이 항목의 내용
DF
각 SS(제곱합)에 대한 자유도(DF)입니다. 일반적으로 자유도는 각 SS를 계산하는 데 사용할 수 있는 정보의 양을 측정합니다.
SS
제곱합(SS)은 거리 제곱의 합이며, 여러 요인으로 인한 변동성의 측도입니다. 총 제곱합은 전체 평균으로 인한 데이터의 변동 양을 나타냅니다. SS 측정 시스템은 각 측정 시스템의 평균 측정값과 전체 평균 간의 변동 양을 나타냅니다.
총 제곱합 = SS 부품 + SS 측정 시스템 + SS 측정 시스템 * 부품 + SS 반복성
MS
평균 제곱(MS)은 요인이 다른 데이터의 변동입니다. 요인이 다른 경우 수준의 수가 다르거나 가능한 값이 서로 다르다는 사실을 고려합니다.
MS = 각 변동 요인에 대한 SS/DF
F
F-통계량은 측정 시스템, 부품 또는 측정 시스템*부품의 효과가 통계적으로 유의한지 여부를 확인하는 데 사용됩니다.
F-통계량이 클수록 해당 요인이 반응 또는 측정 변수의 변동성에 상당한 영향을 미치는 경향이 있습니다.
P
p-값은 귀무 가설이 참일 경우 최소한 표본에서 계산된 값만큼 극단적인 검정 통계량(예: F-통계량)을 얻을 확률입니다.
해석
평균 측정값이 유의하게 다른지 여부를 확인하려면 분산 분석표의 p-값을 사용합니다. 분산 분석표는 분석 방법에 대해 분산 분석 옵션을 선택한 경우에만 표시됩니다.
낮은 p-값은 모든 부품, 측정 시스템 또는 교호작용이 동일한 평균을 공유한다는 가정이 참이 아닐 수도 있음을 나타냅니다.
- p-값 ≤ α: 하나 이상의 평균이 통계적으로 다름
- p-값이 유의 수준보다 작거나 같으면 귀무 가설을 기각하고 하나 이상의 평균이 다른 평균과 유의하게 다르다는 결론을 내립니다. 예를 들어, 하나 이상의 측정 시스템이 다르게 측정합니다.
- p-값 > α: 평균이 유의하게 서로 다르지 않음
- p-값이 유의 수준보다 크거나 같으면 모집단 평균이 서로 다르다는 결론을 내릴 수 있는 충분한 증거가 없기 때문에 귀무 가설을 기각할 수 없습니다. 예를 들어, 여러 측정 시스템이 서로 다르게 측정한다는 결론을 내릴 수 없습니다.
분산 성분
분산 성분은 분석 분석 표의 각 요인에 대한 추정 분산 성분입니다.
해석
측정 오차의 요인별 변동을 평가하려면 분산 성분을 사용합니다.
양호한 측정 시스템에서는 가장 큰 변동 성분이 부품-대-부품 변동입니다. 반복성과 재현성이 변동량에 크게 기여하는 경우 문제의 원인을 조사하고 수정 조치를 취해야 합니다.
%기여(분산 성분)
%기여는 전체 변동 중 각 분산 성분으로 인한 변동의 백분율입니다. %기여는 각 요인에 대한 분산 성분을 총 변동으로 나눈 다음, 백분율로 표현하기 위해 100을 곱하여 계산합니다.
해석
측정 오차의 요인별 변동을 평가하려면 %기여를 사용합니다.
양호한 측정 시스템에서는 가장 큰 변동 성분이 부품-대-부품 변동입니다. 반복성과 재현성이 변동량에 크게 기여하는 경우 문제의 원인을 조사하고 수정 조치를 취해야 합니다.
표준 편차(SD)
표준 편차(SD)는 각 변동 요인에 대한 표준 편차입니다. 표준 편차는 해당 요인에 대한 분산 성분의 제곱근과 같습니다.
표준 편차는 부품 측정값 및 공차와 단위가 같기 때문에 편리한 변동 측도입니다.
연구 변동(6 * SD)
연구 변동은 각 변동 요인에 대한 표준 편차에 6 또는 사용자가 연구 변동에서 지정하는 승수를 곱하여 계산합니다.
일반적으로 공정 변동은 6s로 정의되는데, 여기서 s는 표준 편차이며 모집단 표준 편차(σ 또는 시그마로 표시됨)의 추정치입니다. 데이터가 정규 분포를 따르는 경우 데이터의 약 99.73%가 평균의 6 표준 편차 내에 포함됩니다. 데이터의 다른 백분율을 정의하려면 표준 편차의 다른 배수를 사용합니다. 예를 들어, 데이터의 99%가 어디 포함되는지 확인하려면 기본 배수 6 대신 배수 5.15를 사용합니다.
%연구 변동(%SV)
%연구 변동은 각 변동 요인에 대한 연구 변동을 총 변동으로 나눈 후 100을 곱하여 계산합니다.
%연구 변동은 해당 요인에 대해 계산된 분산 성분의 제곱근입니다. 따라서 분산 성분 값의 %기여 합은 100이지만 %연구 변동의 합은 그렇지 않습니다.
해석
측정 시스템 변동을 총 변동과 비교하려면 %연구 변동을 사용합니다. 측정 시스템을 사용하여 부품별 변동 감소와 같은 공정 개선을 평가하는 경우, %연구 변동이 측정 정밀도의 더 나은 추정치입니다. 규격과 비교하여 부품을 평가하기 위해 측정 시스템의 공정 능력을 평가하는 경우에는 %공차가 적절한 측도입니다.
%공차(SV/공차)
%공차는 각 요인에 대한 연구 변동을 공정 공차로 나누고 100을 곱하여 계산합니다.
공차를 입력하는 경우, Minitab에서는 측정 시스템 변동을 규격과 비교하는 %공차를 계산합니다.
해석
규격과 비교하여 부품을 평가하려면 %공차를 사용합니다. 부품별 변동 감소와 같은 공정 개선을 위해 측정 시스템을 평가하는 경우, %연구 변동이 적절한 측도입니다.
%공정(SV/공정변동)
사용자가 과거 표준 편차를 입력하지만 연구에 포함된 부품을 사용하여 공정 변동을 추정하는 경우 Minitab에서는 %공정을 계산합니다. %공정은 측정 시스템 변동을 과거 표준 편차와 비교합니다. %공정은 각 요인에 대한 연구 변동을 과거 공정 변동으로 나눈 다음 100을 곱하여 계산합니다. 기본적으로 공정 변동은 과거 표준 편차에 6을 곱한 것과 같습니다.
사용자가 과거 표준 편차를 사용하여 공정 변동을 추정하는 경우 Minitab에서는 %공정이 %연구 변동과 같기 때문에 %공정을 표시하지 않습니다.
95% CI
95% 신뢰 구간(95% CI)은 각 측정 오차 측도의 실제 값이 포함될 가능성이 있는 값의 범위입니다.
Minitab에서는 분산 성분, 분산 성분의 %기여, 표준 편차, 연구 변동, %연구 변동, %공차, 구별 범주의 수에 대한 신뢰 구간을 제공합니다.
해석
데이터 표본이 랜덤이기 때문에 두 Gage 연구에서 동일한 신뢰 구간이 생성될 가능성은 없습니다. 그러나 연구를 여러 번 반복할 경우 일정 비율의 결과 신뢰 구간에 알 수 없는 실제 측정값 오차가 포함됩니다. 모수를 포함하는 이러한 신뢰 구간의 백분율이 해당 구간의 신뢰 수준입니다.
예를 들어, 95% 신뢰 수준에서 신뢰 구간에 실제 값이 포함된다고 95% 확신할 수 있습니다. 신뢰 구간은 결과의 실제 유의성을 평가하는 데 도움이 됩니다. 해당 상황에 실제적으로 유의한 값이 신뢰 구간에 포함되는지 여부를 확인하려면 전문 지식을 사용하십시오. 신뢰 구간이 너무 넓어서 유의하지 않은 경우에는 표본 크기를 늘려보십시오.
반복성에 대한 분산 성분이 0.044727이고 이에 해당하는 95% 신뢰 구간이 (0.035, 0.060)이라고 가정합니다. 반복성으로 인한 변동의 추정치는 데이터에서 0.044727로 계산됩니다. 0.035에서 0.060의 구간에 반복성으로 인한 실제 변동이 포함된다고 95% 확신할 수 있습니다.
구별 범주의 수
구별 범주의 수는 Gage R&R 연구에서 측정된 특성의 차이를 탐지하는 측정 시스템의 능력을 식별하기 위해 사용하는 측도입니다. 구별 범주의 수는 사용자가 선택한 표본에 의해 정의되는, 제품의 변동 범위에 걸쳐 나타나는 겹치지 않는 신뢰 구간의 개수를 나타냅니다. 구별 범주의 수는 측정 시스템이 공정 데이터 내에서 식별할 수 있는 그룹의 수도 나타냅니다.
해석
Automobile Industry Action Group(AIAG)에서 발행한 Measurement Systems Analysis Manual1에 따르면 5개 이상의 범주가 허용 가능한 측정 시스템을 나타냅니다. 구별 범주의 수가 5 미만일 경우 측정 시스템에서 충분한 해를 가지지 못할 수도 있습니다.
일반적으로 구별 범주의 수가 2보다 작으면 부품을 구별할 수 없기 때문에, 측정 시스템이 공정을 제어하지 못합니다. 구별 범주의 수가 2인 경우에는 부품을 높음, 낮음과 같이 두 그룹으로 나눌 수 있습니다. 구별 범주의 수가 3인 경우에는 부품을 높음, 중간, 낮음과 같이 세 그룹으로 나눌 수 있습니다.
자세한 내용은 구별 범주의 수 사용에서 확인하십시오.
오분류 확률
하나 이상의 규격 한계를 지정하면 Minitab에서 제품 오분류 확률을 계산할 수 있습니다. Gage 변동으로 인해 측정된 부품 값이 항상 부품의 실제 값과 같은 것은 아닙니다. 측정된 값과 실제 값이 일치하지 않기 때문에 제품이 오분류될 가능성이 있습니다.
- 결합 확률
- 부품의 합격 가능성에 대한 사전 지식이 없는 경우 결합 확률을 사용합니다. 예를 들어, 생산 라인에서 표본을 추출하고 특정 부품이 좋은지 또는 나쁜지 알지 못합니다. 다음과 같은 두 가지의 오분류가 있습니다.
- 부품이 불량이지만 해당 부품을 합격시킬 확률.
- 부품이 양호하지만 해당 부품을 기각시킬 확률.
- 조건부 확률
- 부품의 합격 가능성에 대한 사전 지식이 있는 경우 조건부 확률을 사용합니다. 예를 들어, 재작업할 더미 또는 곧 배송될 제품 더미에서 표본을 추출합니다. 다음과 같은 두 가지의 오분류가 있습니다.
- 재작업이 필요한 불량 제품 더미에서 추출된 부품을 합격시킬 확률(잘못된 합격이라고도 함).
- 곧 배송될 양호 제품 더미에서 추출된 부품을 기각시킬 확률(잘못된 기각이라고도 함).
해석
결합 확률
| 설명 | 확률 |
|---|---|
| 랜덤하게 선택된 부품이 불량인데 합격되었습니다 | 0.037 |
| 랜덤하게 선택된 부품이 양호한데 기각되었습니다 | 0.055 |
조건부 확률
| 설명 | 확률 |
|---|---|
| 불량 제품 그룹의 부품이 합격되었습니다 | 0.151 |
| 양호 제품 그룹의 부품이 기각되었습니다 | 0.073 |
부품이 불량이지만 해당 부품을 합격시킬 결합 확률은 0.037입니다. 부품이 양호하지만 해당 부품을 기각시킬 결합 확률은 0.055입니다.
잘못된 합격, 즉 부품이 실제로 규격을 벗어나지만 재검사 시 해당 부품을 합격시킬 조건부 확률은 0.151입니다. 잘못된 기각, 즉 부품이 규격 한계에 포함되지만 재검사 시 해당 부품을 기각시킬 조건부 확률은 0.073입니다.
VDA 5
참고
VDA 5는 웹 앱에만 있습니다.
참고
이 분석은 uEVR, uRE 및 uEVO 간의 최대 불확실성을 사용하여 측정 프로세스의 변동을 계산합니다. 다른 2개 통계의 합계 비율은 해당 통계가 합계에 기여하지 않기 때문에 누락되었습니다.
- 교정(uCAL)
- 교정(uCAL)은 참조 표준의 교정으로 인한 측정의 불확실성입니다. 이 통계는 분석에 대한 입력입니다. 일반적으로 이 값은 교정 인증서에서 가져옵니다.
- 기준 시 반복성(uEVR)
- 참조 시 반복성(uEVR)은 동일한 작업자가 동일한 장치를 사용하여 기준 부품을 반복적으로 측정하여 발생하는 불확실성입니다. 이 통계는 분석에 대한 입력입니다. 일반적으로 이 값은 Type I 게이지 연구에서 가져옵니다.
- 해(uRE)
- 해(uRE)은 게이지의 분해능으로 인한 불확실성입니다. 분석은 게이지의 분해능이 분석에 대한 입력일 때 이 통계를 계산합니다.
- 측정 대상의 반복성(uEVO)
- 측정 대상의 반복성(uEVO)은 Gage R&R 연구의 반복성으로 인한 불확실성입니다. 반복성은 동일한 작업자가 동일한 부품을 여러 번 측정할 때 측정의 변동성입니다.
- 치우침(uBI)
- 치우침(uBI)는 알려진 참조 측정값과의 차이와 연구에서 측정값의 평균으로 인한 측정의 불확실성입니다. 이 통계는 분석에 대한 입력입니다. 일반적으로 이 값은 참조 부분이 측정 범위 내에 있는 편향 연구에서 가져옵니다.
- 선형성(uLIN)
- 선형성(uLIN)은 선형성으로 인한 측정의 불확실성입니다. 선형성은 부품 값이 변경됨에 따라 바이어스의 변화로 인해 발생하는 참조 부품의 값과 평균 측정값 간의 차이입니다. 이 통계는 분석에 대한 입력입니다. 일반적으로 이 값은 참조 부품이 측정 범위 내에 있는 선형성 연구에서 가져옵니다.
- 다른 요인들(uREST)
- 다른 요인들(uREST)은 하나 이상의 추가 요인으로 인한 측정의 불확실성입니다. 분석 사양에 한 가지 추가 요인이 있는 경우 이 불확실성은 분석에 대한 입력입니다. 분석 사양에 둘 이상의 요인이 있는 경우 이 불확실성은 값을 결합합니다. 예를 들어, 데이터 수집이 더 높은 온도에 있을 때 측정값의 차이가 더 큰 경우 온도로 인한 불확실성을 설명하기 위해 다른 요인에 대한 사양을 사용합니다.
- 운영자(uAV)
- 운영자(uAV)는 Gage R&R 연구의 재현성으로 인한 측정의 불확실성입니다. 재현성은 서로 다른 작업자가 동일한 부품을 측정할 때 측정의 가변성입니다.
- 상호 작용(uIA)
- 상호 작용(uIA)은 Gage R&R 연구에서 부품과 작업자 간의 상호 작용으로 인한 측정의 불확실성입니다. Part*Operator 상호 작용이 ANOVA 테이블에서 통계적으로 유의할 때 상호 작용이 분석에 포함됩니다.
- 측정 프로세스(uMP)
- 측정 프로세스(uMP)는 모든 불확도 구성 요소를 결합하여 측정 프로세스의 총 불확도를 추정합니다.
- 총계의 %
- 각 불확실성 원인에 대해 분석은 해당 원인에서 발생하는 uMP의 백분율을 나타냅니다. 백분율을 사용하여 다양한 소스의 불확실성의 양을 비교합니다.
- 허용 오차의 % (%QMP)
- 공차 비율(%QMP)은 측정 공정의 불확실성과 연구 변동을 결합하고 값을 공정 공차와 비교합니다. %QMP는 측정 프로세스가 만족스러운지 결정하는 일반적인 방법입니다. 일부 응용 프로그램에서 30% 이하의 값은 측정 프로세스가 만족스럽다는 것을 나타냅니다.
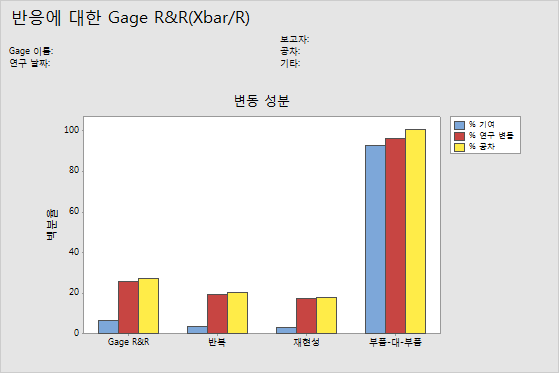
분산 성분 그래프
분산 성분 차트는 Gage R&R 연구 결과를 그래픽으로 요약한 것입니다.
- 총 Gage R&R: 동일한 Gage를 사용하는 여러 측정 시스템이 포함된 측정 시스템의 변동성.
- 반복성: 동일한 부품을 동일한 측정 시스템에서 여러 번 측정할 경우 측정값의 변동성.
- 재현성: 동일한 부품을 서로 다른 측정 시스템에서 측정할 경우 측정값의 변동성.
- 부품-대-부품: 서로 다른 부품으로 인한 측정값의 변동성.
해석
- %기여
- %기여는 전체 변동 중 각 분산 성분으로 인한 변동의 백분율입니다. %기여는 각 요인에 대한 분산 성분을 총 변동으로 나눈 다음, 100을 곱하여 계산합니다.
- %연구 변동
- %연구 변동은 각 요인으로 인한 연구 변동의 백분율입니다. %연구 변동은 각 요인에 대한 연구 변동을 총 연구 변동으로 나눈 다음, 100을 곱하여 계산합니다.
- %공차
- %공차는 측정 시스템 변동을 규격과 비교합니다. %공차는 각 요인에 대한 연구 변동을 공정 공차로 나눈 다음, 100을 곱하여 계산합니다.
- %공정
- %공차는 측정 시스템 변동을 총 변동과 비교합니다. %공차는 각 요인에 대한 연구 변동을 과거 공정 변동으로 나눈 다음, 100을 곱하여 계산합니다.
양호한 측정 시스템에서 가장 큰 변동 성분은 부품-대-부품 변동입니다.
R 관리도
R 관리도는 측정 시스템 일관성을 표시하는 범위의 관리도입니다.
- 표시된 점
- 각 측정 시스템이 각 부품에 대해 측정한 최대값과 최소값 간의 차이입니다. R 관리도는 측정 시스템별로 점을 표시하기 때문에 각 측정 시스템의 일관성을 살펴볼 수 있습니다.
- 중심선(Rbar)
- 공정의 전체 평균(즉, 모든 표본 범위의 평균)입니다.
- 관리 한계(LCL과 UCL)
- 표본 범위에 대해 기대할 수 있는 변동량입니다. 관리 한계 계산에는 표본 내 변동이 사용됩니다.
참고
각 측정 시스템에서 각 부품을 9번 이상 측정하는 경우 R 관리도 대신 S 관리도가 표시됩니다.
해석
작은 평균 범위는 측정 시스템의 변동성이 낮다는 것을 나타냅니다. 관리 상한(UCL)보다 높은 점은 측정 시스템에서 부품을 일관되게 측정하지 않음을 나타냅니다. UCL 계산에는 각 측정 시스템의 부품당 측정 횟수와 부품 간 변동이 포함됩니다. 측정 시스템에서 부품을 일관되게 측정할 경우, 최대 측정값과 최소 측정값 간의 범위가 연구 변동에 비해 작고 점이 관리 상태에 있습니다.
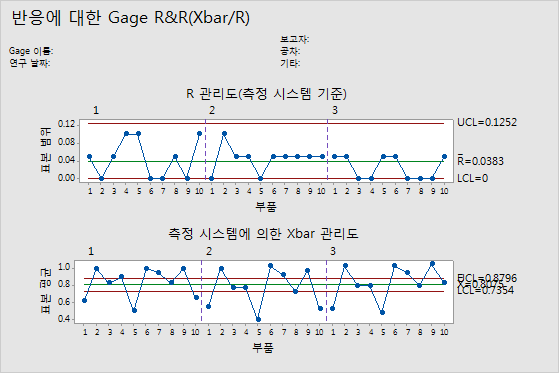
Xbar 관리도
Xbar 관리도는 부품-대-부품 변동을 반복성 성분과 비교합니다.
- 표시된 점
- 각 측정 시스템별로 표시되는 각 부품의 평균 측정값입니다.
- 중심선(Xbar)
- 모든 측정 시스템에서 측정한 모든 부품 측정값의 전체 평균입니다.
- 관리 한계(LCL과 UCL)
- 관리 한계는 반복성 추정치와 각 평균의 측정값 수를 바탕으로 한 값입니다.
해석
Gage R&R 연구를 위해 선택된 부품은 가능한 부품의 전체 범위를 나타냅니다. 따라서 이 그래프는 반복성에서만 예상되는 변동이 부품 평균 간 변동을 더 많이 나타냅니다.
이상적으로 그래프는 관리 한계가 좁고 측정 시스템의 변동성이 낮음을 나타내는 관리 이탈 상태의 점이 많습니다.

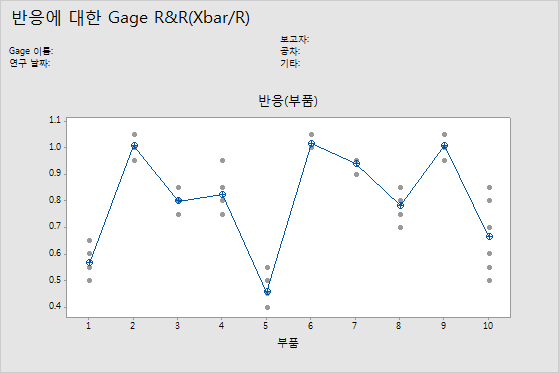
부품별 그래프
이 그래프에는 요인 수준 간의 차이가 표시됩니다. Gage R&R 연구는 일반적으로 부품 및 측정 시스템별로 측정값을 정렬합니다. 그러나 Gage R&R (확장) 연구에서는 다른 요인도 그래프로 표시할 수 있습니다.
그래프에서 점은 측정값을 나타내며 원-십자 기호는 평균을 나타냅니다. 연결 선은 각 요인 수준에 대한 평균 측정값을 연결합니다.
참고
수준당 관측치가 9개보다 많은 경우에는 개별 값 그림 대신 상자 그림이 표시됩니다.
해석
각 개별 부품에 대한 여러 측정값이 거의 변하지 않으면(한 부품에 대한 점들이 서로 가까우면) 측정 시스템의 변동이 낮다는 것을 나타냅니다. 또한 부품이 서로 다르고 공정의 전체 범위를 나타낸다는 것을 보여주기 위해 부품의 평균 측정값이 충분히 변동해야 합니다.
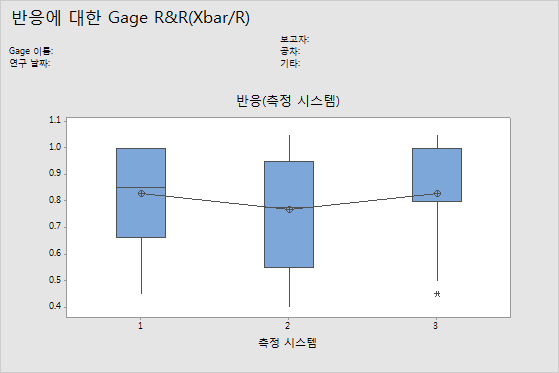
측정 시스템별 그래프
측정 시스템별 관리도에는 연구에 사용된 모든 측정값이 측정 시스템별로 정렬되어 표시됩니다. 이 그래프에는 요인 수준 간의 차이가 표시됩니다. Gage R&R 연구는 일반적으로 부품 및 측정 시스템별로 측정값을 정렬합니다. 그러나 Gage R&R (확장) 연구에서는 다른 요인도 그래프로 표시할 수 있습니다.
참고
측정 시스템당 관측치가 10개 미만인 경우에는 상자 그림 대신 개별 값 그림이 표시됩니다.
해석
측정 시스템에 걸친 수평선은 각 측정 시스템에 대한 평균 측정값이 유사하다는 것을 나타냅니다. 이상적으로 각 측정 시스템에 대한 측정값의 변화는 동일합니다.
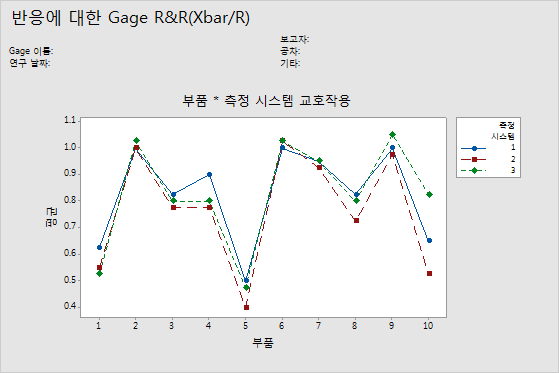
측정 시스템*부품 교호작용 그래프
측정 시스템*부품 교호작용 그래프에는 각 측정 시스템의 각 부품에 대한 평균 측정값이 표시됩니다. 각 선은 단일 측정 시스템(또는 사용자가 지정한 항)에 대한 평균을 연결합니다.
교호작용도는 두 요인 간의 교호작용을 표시합니다. 교호작용은 한 요인의 효과가 두 번째 요인에 따라 달라질 때 발생합니다. 이 그림은 분산 분석표의 교호작용 항에 대한 F-검정과 유사합니다.
해석
일치하는 선은 여러 측정 시스템이 서로 유사하게 측정한다는 것을 나타냅니다. 평행하지 않거나 교차하는 선은 측정 시스템의 부품 측정 능력이 측정 중인 부품에 따라 일관되게 달라진다는 것을 나타냅니다. 다른 선보다 일관되게 높거나 낮은 선은 측정 시스템에서 일관되게 높거나 낮게 측정하여 측정값에 치우침을 추가한다는 것을 나타냅니다.