Gage R&R (교차) 연구 예

한 엔지니어가 공정 변동의 기대 범위를 나타내는 부품 10개를 선택합니다. 측정 시스템 세 대에서 부품 10개를 부품당 세 번씩 랜덤 순서로 측정합니다.

엔지니어가 측정 시스템으로 인한 측정값의 변동성을 평가하기 위해 Gage R&R 연구(교차)를 수행합니다.

표본 데이터를 엽니다 Gage데이터.MWX.
통계분석 > 품질 도구 > Gage 연구 > Gage R&R (교차) 연구을 선택합니다.
시료 번호에 부품을 입력합니다.
측정 시스템에 조작자을 입력합니다.
측정 데이터에 측정값을 입력합니다.
분석 방법 아래에서 분산 분석을 선택합니다.
옵션 버튼을 클릭합니다. 공정 공차 아래에서 규격 상한 - 규격 하한을 선택하고 8을 입력합니다.
각 대화 상자에서 확인을 클릭합니다.

결과 해석

이원 분산 분석표에는 부품, 측정 시스템 및 부품-측정 시스템 교호작용에 대한 항이 포함됩니다. 교호작용에 대한 p-값이 0.05 이상인 경우, Minitab에서는 교호작용이 유의하지 않기 때문에 교호작용을 완전 모형에서 제외합니다. 이 예에서 p-값은 0.974이므로, Minitab에서는 최종 모형에서 교호작용을 제외한 두 번째 이원 분산 분석표를 생성합니다.

각 측정 오차의 요인별 변동을 총 변동에 비교하려면 분산 성분(CarComp)을 사용합니다. 이 결과에서 Gage R&R 표의 %기여 열에는 부품-대-부품 변동이 92.24%로 표시되어 있습니다. 이 값은 7.76%인 총 Gage R&R보다 훨씬 더 큽니다. 따라서 많은 변동이 부품 간의 차이로 인해 발생합니다.

측정 시스템 변동을 총 변동과 비교하려면 %연구 변동을 사용합니다. 총 Gage R&R은 연구 변동의 27.86%입니다. 응용 분야에 따라 총 Gage R&R %기여가 허용될 수 있습니다. 자세한 내용은 측정 시스템의 허용 가능 여부에서 확인하십시오.

이 데이터의 경우 구별 범주의 수가 4개입니다. AIAG 방법에 따르면 측정 시스템이 적절한 것이 되려면 구별 범주의 수가 5개 이상이어야 합니다. 자세한 내용은 Gage R&R 연구에서 구별 범주 수 사용에서 확인하십시오.

그래프는 측정 시스템에 대한 다음과 같은 정보도 제공합니다.

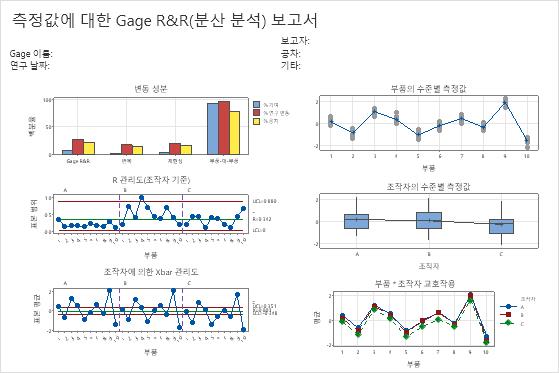
분산 성분 그래프에서 부품-대-부품 변동으로 인한 %기여가 총 Gage R&R의 %기여보다 큽니다. 따라서 많은 변동이 부품 간의 차이로 인해 발생합니다.
측정 시스템별 R 관리도는 측정 시스템 B에서 부품을 일관되지 않게 측정한다는 것을 보여줍니다.
측정 시스템별 Xbar 관리도에서는 대부분의 점이 관리 한계를 벗어납니다. 따라서 많은 변동이 부품 간의 차이로 인해 발생합니다.
부품별 그래프는 부품 간의 차이가 크다는 것을 보여줍니다.
측정 시스템별 그래프에서는 측정 시스템 간 차이가 부품 간 차이보다 작지만 유의합니다(p-값 = 0.00). 측정 시스템 C의 측정값이 다른 측정 시스템의 측정값보다 약간 작은 경향이 있습니다.
측정 시스템*부품 교호작용 그래프에서는 선이 거의 평행하며 표에 있는 측정 시스템*부품 교호작용에 대한 p-값은 0.974입니다. 이 결과는 각 부품과 측정 시스템 간에 유의한 교호작용이 없다는 것을 나타냅니다.

교호작용이 있는 이원 분산 분석표

출처	DF	SS	MS	F	P
부품	9	88.3619	9.81799	492.291	0.000
조작자	2	3.1673	1.58363	79.406	0.000
부품 * 조작자	18	0.3590	0.01994	0.434	0.974
반복성	60	2.7589	0.04598
총계	89	94.6471

교호작용이 없는 이원 분산 분석표

출처	DF	SS	MS	F	P
부품	9	88.3619	9.81799	245.614	0.000
조작자	2	3.1673	1.58363	39.617	0.000
반복성	78	3.1179	0.03997
총계	89	94.6471

분산 성분

출처	분산 성분	%기여(분산 성분)
총 Gage R&R	0.09143	7.76
반복성	0.03997	3.39
재현성	0.05146	4.37
조작자	0.05146	4.37
부품-대-부품	1.08645	92.24
총 변동	1.17788	100.00

공정 공차 = 8

Gage 평가

출처	표준 편차(SD)	연구 변동 (6 × SD)	%연구 변동(%SV)	%공차(SV/공차)
총 Gage R&R	0.30237	1.81423	27.86	22.68
반복성	0.19993	1.19960	18.42	14.99
재현성	0.22684	1.36103	20.90	17.01
조작자	0.22684	1.36103	20.90	17.01
부품-대-부품	1.04233	6.25396	96.04	78.17
총 변동	1.08530	6.51180	100.00	81.40

구별 범주의 수 = 4