치우침
치우침은 기준 부품의 알려진 표준 값과 관측된 측정값 평균의 차이로 계산됩니다.
- 공차 하한을 사용한 치우침의 점 추정치
- 치우침 = 하한 + 절편 / 기울기
- 공차 상한을 사용한 치우침의 점 추정치
- 치우침 = 상한 + 절편 / 기울기
두 공식에 대한 절편과 기울기는 확률도의 적합선에서 가져옵니다.
Minitab에서는 기준 값 XT에서 z–점수 Φ-1(확률(합격))을 회귀 분석하여 절편과 기울기를 계산합니다.
사전 수정된 반복성
사전 수정된 반복성은 과도 추정에 대한 수정을 하기 전에 계산되는 반복성입니다.
공식
Minitab에서는 다음 공식을 사용하여 사전 수정된 반복성을 추정합니다.

표기법
| 용어 | 설명 |
|---|---|
| XT | 확률도의 적합선에서 계산된 0.995 및 0.005의 합격 확률에서 추정된 기준 값을 나타냅니다. |
반복성
반복성은 Gage로 인한 측정 시스템의 변동량입니다. 계수형 Gage 분석에서는 기준 값에 대한 합격 확률을 회귀 분석하여 반복성을 계산합니다.
사전 수정된 반복성은 과도 추정에 대한 수정을 하기 전에 계산되는 반복성입니다. Minitab에서는 반복성 추정치를 조정 인수 1.08로 나누어 수정된 반복성을 계산합니다.
공식
Minitab에서는 다음 공식을 사용하여 반복성을 추정합니다.
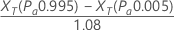
표기법
| 용어 | 설명 |
|---|---|
| XT | 확률도의 적합선에서 계산된 0.995 및 0.005의 합격 확률에서 추정된 기준 값을 나타냅니다. |
분모 1.08은 Automotive Industry Action Group1에 의해 지정된 조정 인수입니다. Minitab은 수정된 반복성 값을 사용하여 치우침이 0인지 검사합니다.
AIAG 방법에 대한 T
공식
회귀 방법을 사용하여 치우침 = 0을 검정하기 위해 Minitab에서는 다음 공식을 사용합니다.
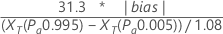
표기법
| 용어 | 설명 |
|---|---|
| XT | 확률도의 적합선에서 계산된 0.995 및 0.005의 합격 확률에서 추정된 기준 값을 나타냅니다. |
- 합격 횟수가 0보다 크고 20보다 작은 부품 6개
- 합격 횟수가 0인 부품 1개
- 합격 횟수가 20인 부품 1개
회귀 방법에 대한 T
공식
회귀 방법을 사용하여 치우침 = 0을 검정하기 위해 Minitab에서는 다음 공식을 사용합니다.
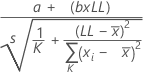
표기법
| 용어 | 설명 |
|---|---|
| a | 확률도의 적합선 절편 |
| b | 확률도의 적합선 기울기 |
| LL | 공차 하한 |
| s | 적합선을 사용하여 계산된 오차 표준 편차 |
| K | 부품 수 |
| xi | 각 부품의 기준 값 |
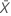 | 기준 값의 평균 |
AIAG 방법의 자유도
자유도는 p-값을 계산하는 데 사용됩니다.
DF = N – 1.
표기법
| 용어 | 설명 |
|---|---|
| N | 시행 횟수 |
회귀 방법의 자유도
자유도는 p-값을 계산하는 데 사용됩니다.
DF = N – 2.
표기법
| 용어 | 설명 |
|---|---|
| N | 적합선을 얻기 위해 사용되는 점의 개수 |
p-값
p-값은 귀무 가설을 기각하거나 받아들이는 가설 검정에서 사용됩니다.
측정 시스템의 치우침이 통계적으로 유의한지 여부를 확인하려면 p-값을 유의 수준과 비교하십시오. 일반적으로 0.05의 유의 수준(α 또는 알파로 표시함)이 적절합니다. 0.05의 유의 수준은 유의한 치우침이 없는데 치우침이 존재한다는 결론을 내릴 위험이 5%라는 것을 나타냅니다.
적합선
적합선은 합격 확률과 측정된 부품의 기준 값 간의 관계를 검사하는 회귀선입니다.
적합선의 일반적인 형태는 다음과 같습니다. Y = b0 + b1 X
Minitab에서는 기준 값 XT에서 z–점수 Φ-1(확률(합격))을 회귀 분석하여 절편과 기울기를 얻습니다.
표기법
| 용어 | 설명 |
|---|---|
| b0 | 절편 - 회귀선이 세로 축과 만나는 지점을 결정하는 상수 |
| b1 | 회귀선의 기울기 |
| X | 예측 변수 값 |
적합선에 대한 R-제곱
적합선에 대한 R-제곱은 적합선이 데이터를 제대로 모형화하는지 여부를 확인하기 위해 사용되는 결정 계수입니다. 적합선에 대한 R-제곱(R2) 값은 합격 반응 확률에서 회귀 모형에 의해 설명되는 변동의 백분율을 나타냅니다.
R2 = 1 - (오차 제곱합 / 총 제곱합)
표기법
| 용어 | 설명 |
|---|---|
| 오차 제곱합 | 오차의 제곱합 |
| 총 제곱합 | 총 제곱합 |
