Kendall의 일치성 계수
Kendall의 통계량은 수준이 세 개 이상인 순서형 데이터와 함께 사용하십시오.
방법 설명에서는 일반성을 잃지 않으면서 각 평가자가 각 대상의 등급을 한 번 매기고 대상마다 k명의 평가자가 있다고 가정합니다. 그런 다음, Kendall의 계수를 계산하기 위해 k명의 평가자가 각 평가자가 시행한 k번의 시행을 나타냅니다.
데이터가 각 행이 특정 평가자가 N개의 대상에 할당한 순위를 나타내는 k x N 표로 정렬되어 있다고 가정합니다.
공식
실제 표준이 알려져 있지 않은 경우 Minitab에서는 다음 공식을 사용하여 Kendall의 계수를 추정합니다.
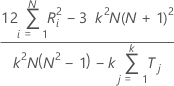
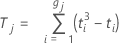
표기법
| 용어 | 설명 |
|---|---|
| N | 대상 수 |
| Σ Ri2 | 순위를 매긴 N개의 대상 각각에 대한 순위 제곱합의 합 |
| K | 평가자 수 |
| Tj | Tj는 같은 값을 갖는 관측치에 등급의 평균을 할당합니다. |
| 용어 | 설명 |
|---|---|
| ti | 같은 값을 갖는 i번째 그룹의 항목 수 |
| gj | j번째 순위 집합에서 같은 값을 갖는 그룹의 수 |
Kendall의 일치성 계수의 유의성 검정
Kendall의 계수의 유의성을 검정하려면 다음 공식을 사용하십시오.
c 2= k (N – 1) W
표기법
| 용어 | 설명 |
|---|---|
| c 2 | 자유도가 N - 1인 카이-제곱 분포를 따릅니다. |
| k | 평가자 수 |
| N | 대상 수 |
| W | 계산된 Kendall의 계수 |
Kendall의 상관 계수
Kendall의 통계량은 수준이 세 개 이상인 순서형 데이터와 함께 사용하십시오.
방법 설명에서는 일반성을 잃지 않으면서 각 평가자가 각 대상의 등급을 한 번 매기고 대상마다 k명의 평가자가 있다고 가정합니다. 그런 다음, k명의 평가자는 Kendall의 상관 계수를 계산하기 위해 모든 평가자가 시행한 k번의 시행을 나타냅니다.
실제 표준을 알고 있는 경우, Minitab에서는 각 평가자와 표준 간 Kendall의 계수 평균을 계산하여 Kendall의 상관 관계를 추정합니다.
알려진 표준을 사용한 시행의 합치도에 대한 Kendall의 상관 계수는 전체 시행에 대한 Kendall 상관 계수의 평균입니다.
공식
Minitab에서는 다음 공식을 사용하여 각 시행과 표준 간의 Kendall의 계수를 계산합니다.

표기법
| 용어 | 설명 |
|---|---|
| TX | X = 0.5 Σi ni+ (ni+– 1)에서 같은 값을 갖는 쌍의 수 |
| TY | Y = 0.5 Σj n+j (n+j– 1)에서 같은 값을 갖는 쌍의 수 |
| C | 일치 쌍의 수 = Σi<kΣj<l nij nkl |
| D | 불일치 쌍의 수 = Σi<kΣj>l nij nkl |
| 용어 | 설명 |
|---|---|
| ni+ | i번째 행의 관측치 수 |
| n+j | j번째 열의 관측치 수 |
| nij | i번째 행과 j번째 열에 해당하는 셀의 관측치 |
| nkl | k번째 행과 l번째 열에 해당하는 셀의 관측치 |
| n++ | 총 관측치 수 |
참고 문헌
A. Agresti (1984). Analysis of Ordinal Categorical Data, John Wiley & Sons.
Kendall의 상관 계수 유의성 검정
공식
실제 표준을 알고 있을 때 Kendall의 계수 유의성을 검정하려면 다음 공식을 사용하십시오.
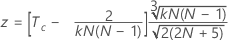
다음 공식을 사용하십시오.
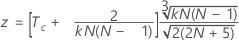
표기법
| 용어 | 설명 |
|---|---|
| Tc | 각 평가자와 표준 간 Kendall 상관 계수의 평균 |
| N | 총 대상 수 |
| k | 평가자 수 |
