시그마(σ)는 공정의 표준 편차입니다. σ의 과거 값을 입력하면 Minitab에서 과거 값을 사용합니다. 그렇지 않은 경우 Minitab에서는 다음 방법 중 하나를 사용하여 데이터에서 σ를 추정합니다.
평균 이동 범위[MR] 방법
평균 이동 범위 
(길이 w)는 다음 공식으로 계산됩니다.
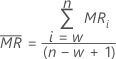
여기서 MRi는 관측치 i에 대한 이동 범위[MR]로, 다음과 같이 계산됩니다.
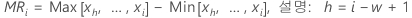
Minitab에서는 
를 사용하여 σ의 불편화 추정치인 Smr를 계산합니다.
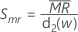
표기법
| 용어 | 설명 |
|---|---|
| n | 관측치 수 |
| w | 이동 범위[MR]의 길이. 기본값은 2입니다. |
| d2() | 괄호 안에 지정된 값에 해당하는 불편화 상수 d2의 값. |
이동 범위[MR]의 중위수 방법
이동 범위[MR]의 중위수 
(길이 w)는 다음 공식으로 계산됩니다.
여기서 MRi는 관측치 i에 대한 이동 범위[MR]로, 다음과 같이 계산됩니다.
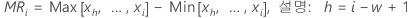
Minitab에서는 
를 사용하여 σ의 불편화 추정치인 Smr를 계산합니다.
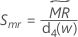
표기법
| 용어 | 설명 |
|---|---|
| n | 관측치 수 |
| w | 이동 범위[MR]의 길이. 기본값은 2입니다. |
| d4() | 괄호 안에 지정된 값에 해당하는 불편화 상수 d4의 값. |
MSSD의 제곱근 방법
MSSD는 연속 차이의 제곱 평균을 나타냅니다. MSSD의 제곱근(SRMSSD)은 다음과 같이 계산됩니다.
불편화 상수 사용
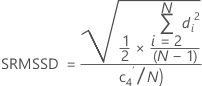
불편화 상수 사용하지 않음
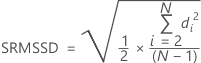
표기법
| 용어 | 설명 |
|---|---|
| di | 관측치 i의 값과 관측치 i – 1의 값의 차이 |
| N | 관측치 수 |
| c4'(N) | 표의 불편화 상수 |
Rbar 방법
Minitab에서는 각 부분군의 범위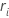 
를 사용하여 
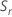(σ의 불편화 추정기)를 계산합니다.
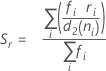
설명
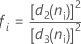
부분군 크기가 일정한 경우 공식은 다음과 같이 단순화됩니다.
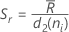
설명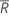 
(Rbar)는 부분군 범위의 평균으로, 다음과 같이 계산됩니다.
표기법
| 용어 | 설명 |
|---|---|
| ri | 부분군 i에 대한 범위 |
| m | 부분군 수 |
| d2(·) | 괄호 안에 지정된 값에 해당하는 불편화 상수 d2의 값. |
| ni | 부분군 i의 관측치 수 |
| d3(·) | 괄호 안에 지정된 값에 해당하는 불편화 상수 d3의 값. |
Sbar 방법
불편화 상수 사용하지 않음
불편화 상수를 사용하지 않는 경우 Sbar는 부분군 표준 편차의 평균입니다.
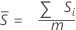
불편화 상수 사용
불편화 상수 c4(ni)를 사용하는 경우 Sbar는 다음과 같이 계산됩니다.
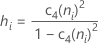
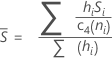
부분군 크기가 일정한 경우 Sbar는 다음과 같이 계산됩니다.
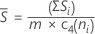
표기법
| 용어 | 설명 |
|---|---|
| c4 (ni) | 괄호 안에 지정된 값에 해당하는 불편화 상수 c4의 값. |
| Si | 부분군 i의 표준 편차 |
| m | 부분군 개수 |
합동 표준 편차 방법
합동 표준 편차(Sp)는 다음 공식으로 계산됩니다.
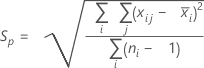
부분군 크기가 일정한 경우 Sp는 다음과 같이 계산됩니다.
불편화 상수 사용
기본적으로 Minitab에서는 합동 표준 편차를 사용하여 σ를 추정할 때 불편화 상수 c4()를 적용합니다.
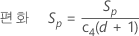
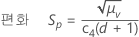
표기법
| 용어 | 설명 |
|---|---|
| xij | i번째 부분군의 j번째 관측치 |
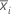 | 부분군 i의 평균 |
| ni | 부분군 i의 관측치 수 |
| μv | 부분군 분산의 평균 |
| c4(·) | 괄호 안에 지정된 값에 해당하는 불편화 상수 c4의 값. |
| d | Sp의 자유도(다음 공식에 의해 계산됨):
 |
