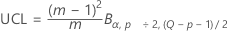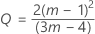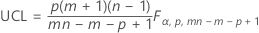원하는 방법 또는 공식을 선택하십시오.
표시된 점
부분군 데이터인 경우
데이터가 부분군에 있는 경우 T2 는 다음과 같이 계산됩니다.
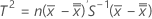
설명:
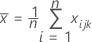
 는 의 평균 벡터입니다.
는 의 평균 벡터입니다. 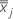 ( xjk 값의 평균)은 다음과 같이 계산됩니다.
( xjk 값의 평균)은 다음과 같이 계산됩니다.
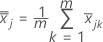
S = 표본 공분산 행렬.
표본 공분산 행렬 S는 다음과 같이 계산됩니다.

설명:
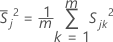
설명:
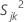 에서 k번째 표본의 j번째 특성에 대한 표본 분산은 다음과 같이 계산됩니다.
에서 k번째 표본의 j번째 특성에 대한 표본 분산은 다음과 같이 계산됩니다.
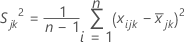
설명:
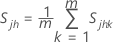
설명:
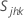 , 공분산 =
, 공분산 =
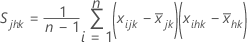
S 행렬의 평균은 공정이 관리 상태에 있을 때 분산의 불편화 추정치입니다. n은 p보다 커야 하며 표본 공분산 행렬이 비정칙이 아니도록 변수 간에 강한 상관 관계가 없어야 합니다.
데이터가 부분군에 있는 경우 관리도는 개별 관측치인 부분군에 대한 결측값을 표시합니다.
데이터가 개별 관측치인 경우
데이터가 개별 관측치인 경우 T2 는 다음과 같이 계산됩니다.
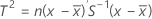
설명:
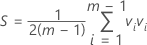
설명:

표기법
| 용어 | 설명 |
|---|---|
| n | 표본 크기 |
 | 표본 평균 벡터 |
| xijk | k번째 샘플에서 j번째 특성에 대한 i번째 관찰 |
| m | 표본 개수 |
T2 계산 예제
Minitab에서는 관리도에 T2 통계량을 표시합니다. 표시된 점이 관리 한계를 초과하면 공정이 이 점에서 관리 한계를 벗어납니다. Minitab 계산에 대해서는 표 및 표본 방정식을 참조하십시오.
다음은 세척액 개발 공정의 데이터입니다. 구연산 나트륨과 글리세린의 양이 세척액의 효능에 영향을 미칩니다.
| 부분군 평균 | 분산 및 공분산 | T2 통계량 | ||||
| 부분군 | 구연산 나트륨(X1) | 글리세린(X2) | S 1 2 | S2 2 | S 1 2 k | T2 |
| 1 | 125 | 025 | 7292 | 8692 | 5791 | 5708 |
| 2 | 625 | 4 | 2292 | 2333 | 3333 | 1429 |
| 3 | 4 | 875 | 1467 | 0625 | 8000 | 9528 |
| 4 | 2 | 2 | 2933 | 7600 | 6667 | 8073 |
| 5 | 25 | 225 | 2500 | 2692 | 7917 | 7548 |
| 6 | 4 | 45 | 6667 | 9567 | 3333 | 2711 |
| 7 | 275 | 025 | 3692 | 4692 | 7108 | 7785 |
| 8 | 6 | 65 | 4333 | 7700 | 6933 | 6183 |
| 9 | 625 | 325 | 7892 | 5558 | 1325 | 3592 |
| 10 | 3 | 5 | 2867 | 9467 | 2600 | 4942 |
| 11 | 25 | 5 | 1767 | 1200 | 9000 | 3279 |
| 12 | 1 | 625 | 1467 | 1692 | 4033 | 0277 |
| 평균 | 7875 | 2333 | 7931 | 9318 | 3003 | |
- 각 변수에 대한 부분군 평균 X1과 X2를 계산합니다. 이 경우 각 부분군에 네 개의 표본이 있습니다.
- 개별 관측치가 있는 경우 Minitab에서는 모든 계산에 부분군 평균 대신 개별 관측치를 사용합니다.
- 부분군 분산 S1 2 및 S2 2를 계산합니다.
- 부분군 공분산 S1 2 k를 계산합니다.
- 부분군 평균의 평균, 부분군 분산의 평균 및 공분산의 평균을 계산합니다.
- 표본 공분산 행렬 S 및 평균 벡터를 지정합니다.
- 다음과 같이 T2을 계산합니다.
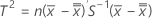
Minitab에서는 T2 관리도에 T2을 표시하고 이를 관리 한계와 비교하여 개별 점이 관리 이탈 상태에 있는지 여부를 확인합니다.
중심선
T2 관리도의 중심선은 KX입니다. K와 X는 Minitab이 데이터에서 공분산 행렬을 추정할 때 최대 표본 크기에 따라 계산됩니다.
부분군 데이터인 경우
부분군 데이터인 경우 KX는 다음과 같이 계산됩니다.
- 지정된 공분산 행렬
-


- 추정 공분산 행렬
-


데이터가 개별 관측치인 경우
데이터가 개별 관측치인 경우 KX는 다음과 같이 계산됩니다.
- 지정된 공분산 행렬
-
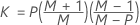
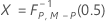
- 추정 공분산 행렬
-
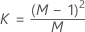
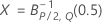
설명:
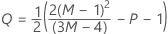
표기법
| 용어 | 설명 |
|---|---|
| P | 변수의 수 |
| M | 부분군 개수 |
| N | 표본 크기 |
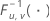 | 분자 자유도가 u이고 분모 자유도가 v인 역 누적 F 분포 |
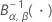 | 첫 번째 형상 모수가 α이고 두 번째 형상 모수가 β인 역 누적 베타 분포 |
관리 한계
부분군 데이터인 경우
모수를 지정하지 않은 경우 관리 상한:
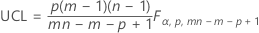
모수를 지정한 경우 관리 상한:
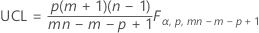
표기법
| 용어 | 설명 |
|---|---|
| α | 고정된 값 0.00134989803156746 |
| p | 특성 수 |
| m |
부분군 데이터인 경우 모수 추정치를 지정하지 않으면 m은 표본의 수입니다. 모수 추정치를 제공하면 m은 공분산 행렬을 생성하기 위해 사용되는 표본의 수입니다. 개체 데이터인 경우 m은 관측치의 수입니다. |
| n | 각 표본의 크기 |
| F | F 분포가 사용된다는 것을 나타냅니다. |
| B | 베타 분포가 사용된다는 것을 나타냅니다. |
Decomposed T2 statistic
분해된 T2 통계량:
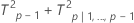
설명:

설명:
xi(p − 1)는 분해된 평균 벡터입니다.
Sxx는 S의 (p – 1) × (p – 1) 주 하위 행렬입니다.
T2p|1,..., p−1은 단계 및 부분군이 있는지 또는 개별 관측치가 있는지 여부에 따라 달라지는 근사입니다.
부분군의 데이터에 대한 1단계:
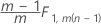
부분군의 데이터에 대한 2단계:
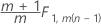
개별 관측치에 대한 1단계:
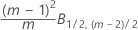
개별 관측치에 대한 2단계:
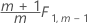
Minitab에서는 모수 추정치가 지정되지 않은 경우 1단계 관리 한계, 지정된 경우 2단계 관리 한계를 계산합니다.
분해된 T2 통계량에 대한 자세한 내용은 Mason et al.2에서 확인하십시오.
표기법
| 용어 | 설명 |
|---|---|
| m | 표본 개수 |
| F | F 분포가 사용된다는 것을 나타냅니다. |
| B | 베타 분포가 사용된다는 것을 나타냅니다. |
Box-Cox 변환에 대한 방법 및 공식
Box-cox 변환 공식
Box-Cox 변환을 사용하는 경우 Minitab에서는 다음 공식에 따라 원래 데이터 값(Yi)을 변환합니다.

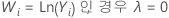
여기서 λ는 변환을 위한 모수입니다. 그런 다음, Minitab에서는 변환된 데이터 값(Wi)에 대한 관리도를 생성합니다. Minitab에서 최적의 λ 값을 선택하는 방법은 Box-Cox 변환에 대한 방법 및 공식에서 확인하십시오.
일반적인 λ 값
| λ | 변환 |
|---|---|
| 2 | 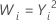 |
| 0.5 |  |
| 0 |  |
| −0.5 | 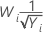 |
| −1 | 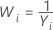 |