표시된 점
다변량 지수가중이동평균[EWMA] 관리도의 표시된 점은 다변량 지수가중이동평균입니다.
해석
공정이 관리 상태에 있을 경우 점들이 관리 상한 아래에 분포하고, 공정은 일반 원인 변동만을 나타냅니다. 관리 상한 위에 있는 점을 조사하십시오. 다변량 관리도의 한 가지 단점은 척도가 변수 척도와 관련이 없고, 관리 이탈 신호가 어떤 변수 또는 변수의 조합으로 인해 관리 이탈 신호가 발생했는지 보여주지 않는다는 것입니다.
관리 한계
관리 상한은 중심선 위의 수평선입니다. 관리 상한은 공정이 관리 이탈 상태에 있는지 여부를 나타내며, 부분군 내의 관측 변동 및 표시된 점들의 기대 변동을 기반으로 합니다.
공분산 행렬
공분산 행렬은 여러 변수에 대한 분산과 공분산을 포함하는 정방형 행렬입니다. 행렬의 대각선 원소는 각 변수의 분산을 포함하며, 대각선 이외의 원소는 가능한 모든 변수 쌍 간의 공분산을 포함합니다.
X와 Y 사이의 공분산은 Y와 X 사이의 공분산과 같기 때문에 분산-공분산 행렬은 대칭입니다. 따라서 각 변수 쌍의 공분산은 행렬에서 두 번씩 나타납니다. i번째 변수와 j번째 변수 사이의 공분산은 (i, j)와 (j, i) 위치에 표시됩니다.
공분산 행렬을 저장한 후 공분산 행렬을 표시하려면 을 선택하십시오.
해석
| X | Y | Z | |
| X | 2.0 | −0.86 | −0.15 |
| Y | −0.86 | 3.4 | 0.48 |
| Z | −0.15 | 0.48 | 0.82 |
분산은 대각선을 따라 굵게 표시됩니다. X, Y, Z의 분산은 각각 2.0, 3.4, 0.82입니다. X와 Y 사이의 공분산은 −0.86, X와 Z 사이의 공분산은 −0.15, Y와 Z 사이의 공분산은 0.48입니다.
단계
특정 시간 동안 공정이 어떻게 변하는지 보여주는 과거 관리도를 만들려면 단계를 사용합니다. 기본적으로 Minitab에서는 각 단계에 대한 중심선과 관리 한계를 다시 계산합니다. 자세한 내용은 단계를 추가하여 공정의 변화 과정 표시에서 확인하십시오.
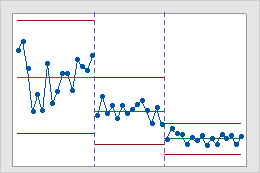
해석
이 과거 관리도는 새 절차 구현 전, 구현 중 및 구현 후를 나타내는 공정의 세 가지 단계를 보여줍니다.