원하는 방법 또는 공식을 선택하십시오.
표시된 점
|Si|는 샘플 i에 대한 표본 공분산 행렬의 행렬식입니다.
부분군이 존재하지 않으면 일반화 분산 관리도에 대한 모든 공식을 계산할 수 없습니다. 이 경우 Minitab에서는 적절한 열 평균을 뺀 다음 모든 데이터 공분산 행렬의 적절한 분산에 대한 제곱근으로 나누어 모든 값을 표준화합니다.
데이터가 부분군에 있는 경우 관리도는 개별 관측치인 부분군에 대한 결측값을 표시합니다. 부분군의 크기가 차트의 변수 수보다 작거나 같은 경우에도 차트에 결측값이 표시됩니다.
Montgomery 1 를 참조하십시오.
중심선
|S|, 표본 공분산 행렬의 행렬식.
관리 한계
관리 하한(LCL)
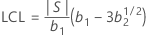
설명:
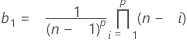
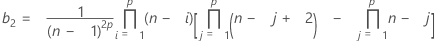
최소 LCL 값은 0입니다.
관리 상한(UCL)
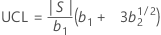
표기법
| 용어 | 설명 |
|---|---|
| p | 변수의 수 |
| n | 각 부분군의 관측치 수 |
Box-Cox 변환에 대한 방법 및 공식
Box-cox 변환 공식
Box-Cox 변환을 사용하는 경우 Minitab에서는 다음 공식에 따라 원래 데이터 값(Yi)을 변환합니다.

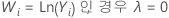
여기서 λ는 변환을 위한 모수입니다. 그런 다음, Minitab에서는 변환된 데이터 값(Wi)에 대한 관리도를 생성합니다. Minitab에서 최적의 λ 값을 선택하는 방법은 Box-Cox 변환에 대한 방법 및 공식에서 확인하십시오.
일반적인 λ 값
다음 표에는 일반적으로 사용되는 λ 값과 변환이 표시됩니다.
| λ | 변환 |
|---|---|
| 2 | 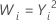 |
| 0.5 |  |
| 0 |  |
| −0.5 | 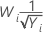 |
| −1 | 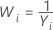 |
1 D.C.참조 Montgomery (2001). Introduction to Statistical Quality Control, 4th edition.John Wiley & Sons
