데이터 변환의 정의
정규 공정 능력 분석 등 정규 데이터용으로 설계된 공정 능력 분석을 사용하는 경우, 데이터가 정규 분포를 따라야 합니다. 데이터가 정규 분포를 따르지 않는 경우 분석 결과가 정확하지 않습니다. 데이터가 더 가깝게 정규 분포를 따르도록 데이터 값을 변경하는 함수를 적용하여 비정규 데이터를 변환할 수 없는 경우도 있습니다.
예를 들어, 피자 배달에 필요한 시간에 대해 공정 능력 분석을 수행하려 한다고 가정합니다. 배달에 필요한 최소 시간이 있지만 최대 배달 시간은 설정되어 있지 않기 때문에 데이터가 오른쪽으로 치우칩니다. 이러한 데이터의 심각한 왜도를 제거하기 위해 변환을 적용할 수 있습니다.
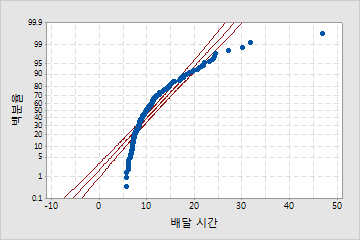
변환 전
피자 배달 시간은 오른쪽으로 치우쳐 있고 정규 분포를 따르지 않는 것으로 보입니다.
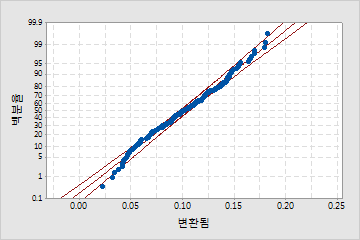
변환 후
데이터를 변환한 후에는 정규 분포를 더 가깝게 따릅니다.
Box-Cox 변환의 기능
Box-Cox 변환은 누승 변환 W = Y**λ으로, 여기서 최적의 λ 값은 Minitab에 의해 결정됩니다.
람다(λ)의 최적 추정치는 -5에서 5 사이의 숫자입니다. 그러나 실제 상황에서는 제곱근(λ=0.5)이나 자연 로그(λ=0)와 같이 이해하기 쉬운 변환에 대응되는 λ 값이 필요합니다.
Johnson 변환의 기능
Johnson 변환은 Box-Cox 변환과 다른 알고리즘을 사용합니다. Johnson 시스템의 세 가지 함수 유형 중에서 Johnson 변환 함수가 선택됩니다. 모수를 변경함으로써 다양한 분포에 해당하는 함수를 제공하기 때문에 대부분 적절한 변환을 찾을 수 있습니다. Minitab에서 선택하는 유형을 최량 변환 유형이라고 부릅니다.
데이터 변환을 사용한 정규 공정 능력 분석 수행
데이터가 비정규 분포를 따를 경우 정규 공정 능력 분석을 사용할 수 있도록 변환을 시도할 수 있습니다.
- 을 선택합니다. 변환을 클릭합니다.
- 변환을 선택합니다.
- Box-Cox 변환
- 이 변환은 이해하기 쉽고 부분군 군내 및 전체 공정 능력 통계량을 모두 제공합니다.
- Johnson 변환
- Johnson 변환은 매우 강력하고 0과 음수가 포함된 데이터에 사용할 수 있지만, 전체 공정 능력 통계량만 제공하는 더 복잡한 변환입니다. Johnson 변환은 Box-Cox 변환을 사용하여 적합한 변환을 찾을 수 없는 경우에 사용합니다.
- 원하는 경우 변환 옵션을 지정한 다음 확인을 클릭합니다.
