Minitab® 지원

정규 Capability Sixpack의 Johnson 변환 데이터에 대한 방법 및 공식

Minitab 에 대해 자세히 알아보기

Johnson 변환 데이터에 대한 공정 능력 지수

Johnson 변환은 세 종류의 변수 분포에서 최적인 함수를 선택합니다. 이는 표준 정규 분포로 쉽게 변환됩니다. 이런 분포는 SB, SL 및 SU로 표시됩니다. 여기서 B, L 및 U는 각각 경계 있는 분포, 대수 정규 분포 및 경계 없는 분포의 변수를 나타냅니다. Minitab에서는 분포에 대한 모수를 첫 번째 형상, 두 번째 형상, 위치 및 척도로 식별합니다. 자세한 내용을 보려면 개별 분포 식별의 변환에 대한 방법 및 공식에서 "Johnson 변환에 대한 방법 및 공식"을 클릭하십시오.

두 규격 한계가 모두 변환 함수의 범위에 있는 경우 Minitab에서는 변환된 데이터에 대한 정규 분포를 기반으로 전체 공정 능력 지수를 계산합니다. 자세한 내용은 정규 공정 능력 분석의 전체 공정 능력 측도에 대한 방법 및 공식에서 확인하십시오.

선택한 모임이 SB 또는 SL 유형이고 규격 하한 및/또는 규격 상한이 분포 범위를 벗어나는 경우 Minitab에서는 전체 공정 능력 지수를 생성하기 위해 추가 계산을 수행합니다.

SB 분포

변환 전에 하나 이상의 규격 한계(X)가 분포 범위를 벗어나는 경우(ε < X < ε + λ이 아님) Pp, Ppk, PPL, PPU, Z.LSL 및 Z.USL은 다음과 같이 계산됩니다.

먼저 Minitab은 변환된 공간에서 백분위수를 계산합니다.

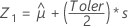
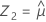
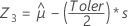
세 개의 Z 값을 사용하여 Minitab은 원래 공간에서 해당하는 X1, X2 및 X3 값을 계산합니다.

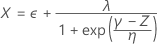
그런 다음 X 값 및 규격 한계 값에서 전체 공정 능력 지수가 계산됩니다.

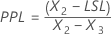
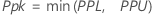
표기법

TermDescription
LSL규격 하한
USL규격 상한
변환된 데이터의 표본 평균(X̅)
Toler표준 편차의 공차
s변환된 데이터의 표본 표준 편차
ε,Johnson 변환의 위치 모수
γJohnson 변환의 형상 모수
ηJohnson 변환의 형상 모수(η >0)
λJohnson 변환의 척도 모수(λ > 0)

SB 분포의 Z.Bench 및 기대 성능 값은 X2 및 분포 한계에 상대적인 LSL 및 USL의 위치에 따라 계산됩니다.

LSL 및 USL이 X2의 반대쪽에 있음
  • LSL과 USL이 모두 분포 범위를 벗어나는 경우 Minitab에서는 다음을 표시합니다.

    Z.Bench가 누락됨

    PPM < LSL = 0

    PPM > USL = 0

    PPM 총계 = 0

  • 한 규격 한계는 분포 범위를 벗어나고 다른 규격 한계는 분포 범위 내에 있는 경우 Minitab에서는 다음 값을 계산합니다.

    범위를 벗어나는 규격 한계에 대한 PPM = 0

    범위 내에 있는 규격 한계에 대한 PPM = p*1000000

    PPM 총계 = p*1000000

    Note

    Minitab에서는 변환된 데이터와 변환된 규격 한계를 사용하여 PPM을 계산합니다.

LSL 및 USL이 X2의 왼쪽에 있음
  • LSL과 USL이 모두 분포 범위를 벗어나는 경우 Minitab에서는 다음을 표시합니다.

    Z.Bench가 누락됨

    PPM < LSL = 0

    PPM > USL = 1

    PPM 총계 = 1

  • LSL이 분포 범위를 벗어나고 USL이 분포 범위 내에 있는 경우 Minitab에서는 다음 값을 계산합니다.

    PPM < LSL = 0

    PPM > USL = p*1000000

    PPM 총계 = PPM > USL

    Note

    Minitab에서는 변환된 데이터와 변환된 규격 한계를 사용하여 PPM을 계산합니다.

LSL 및 USL이 X2의 오른쪽에 있음
  • LSL과 USL이 모두 분포 범위를 벗어나는 경우 Minitab에서는 다음을 표시합니다.

    Z.Bench가 누락됨

    PPM < LSL = 1

    PPM > USL = 0

    PPM 총계 = 1

  • LSL이 분포 범위 내에 있고 USL이 분포 범위를 벗어나는 경우 Minitab에서는 다음 값을 계산합니다.

    PPM < LSL = p*1000000

    PPM > USL = 0

    PPM 총계 = PPM < LSL

    Note

    Minitab에서는 변환된 데이터와 변환된 규격 한계를 사용하여 PPM을 계산합니다.

SL 분포

변환 전에 하나 이상의 규격 한계가 분포 범위를 벗어나는 경우 Minitab에서는 위에 SB 분포에 대해 표시된 것과 같은 방법을 사용하여 Pp, Ppk, PPL, PPU, Z.LSL 및 Z.USL을 계산합니다. 변환된 값 Z로부터 원래 값 X를 찾는 공식만 변경되었습니다.

SL 분포의 Z.Bench 및 기대 성능 값은 ε에 상대적인 LSL 및 USL의 위치에 따라 계산됩니다.
LSL 및 USL이 ε보다 작거나 같음(모두 분포 범위를 벗어남)

Z.Bench가 누락됨

PPM < LSL = 0

PPM > USL = 1

PPM 총계 = 1

LSL이 ε보다 작거나 같음

PPM < LSL = 0

PPM > USL = p*1000000

PPM 총계 = PPM > USL

표기법

TermDescription
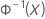표준 정규 분포의 역 누적 분포 함수(CDF)
p변환된 데이터가 변환된 규격 한계를 벗어날 확률
Copyright © 2024 Minitab, LLC. All rights Reserved.