Pp
Pp는 사용자가 지정한 모수 값을 사용하여 계산되거나 분석에 사용된 분포에 대한 최대우도 방법을 사용하여 추정됩니다. Minitab은 에서 선택된 설정에 따라 Z-점수 방법(기본값) 또는 ISO 방법을 사용하여 Pp 통계량을 계산합니다. 다음 공식은 6 표준 편차(공정 평균의 양쪽으로 3 표준 편차씩) 너비인 기본 공차 K = 6을 기반으로 합니다.
Z-점수 방법

표기법
| 용어 | 설명 |
|---|---|
| Zlsl | Φ–1(p1) |
| Zusl | Φ–1(p2) |
| Φ–1(p) | p * 표준 정규 분포의 100번째 백분위수 |
| p1 | Prob (X ≤ LSL) |
| p2 | Prob (X ≤ USL) |
| X | X는 분석에 사용된 분포를 따릅니다. |
ISO 방법

표기법
| 용어 | 설명 |
|---|---|
| USL | 규격 상한 |
| LSL | 규격 하한 |
| X0.99865 | 지정된 분포의 99.865번째 백분위수 |
| X0.00135 | 지정된 분포의 0.135번째 백분위수 |
Ppk

"전체" 기대 성능에 대한 PPM 총계
백만 개의 부품 중에서 규격 한계를 벗어날 것으로 기대되는 부품의 수는 다음과 같이 계산됩니다.
PPM 총계(기대 전체) = PPM < 규격 하한(기대 전체) + PPM > 규격 상한(기대 전체)
PPM 총계(기대 전체) = [1,000,000 * F(규격 하한)]+ [1,000,000 * (1 – F(규격 상한))]
표기법
| 용어 | 설명 |
|---|---|
| F(X) | 추정되거나 지정된 모수를 기반으로 분석에 사용된 분포의 누적 분포 함수(CDF) |
| 규격 하한 | 규격 하한 |
| 규격 상한 | 규격 상한 |
| PPM | 백만 개당 부품 수 |
Z.Bench Z.LSL Z.USL
전체 공정 능력에 대한 벤치마크 Z 통계량은 해당 통계량에 대한 표준 정규 (0, 1) 분포를 사용하여 Z 값을 찾음으로써 계산됩니다.


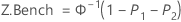
참고
PPL과 PPU는 분석에 사용된 방법(ISO 또는 Minitab)을 기반으로 합니다. 자세한 내용은 비정규 공정 능력 분석의 전체 공정 능력 측도에 대한 방법 및 공식에서 확인하십시오. 공식은 6 표준 편차(공정 평균의 양쪽으로 3 표준 편차씩) 너비인 기본 공차 K = 6을 기반으로 합니다.
표기법
| 용어 | 설명 |
|---|---|
| P1 | 분석에 사용된 비정규 분포 및 사용자가 지정한 모수(또는 데이터에서 추정된 모수)를 기반으로 하는 확률(관측치 < LSL) |
| P2 | 분석에 사용된 비정규 분포 및 사용자가 지정한 모수(또는 데이터에서 추정된 모수)를 기반으로 하는 확률(관측치 > USL) |
| Φ (X) | 표준 정규 분포의 누적 분포 함수(CDF) |
| Φ–1 (X) | 표준 정규 분포의 역 CDF |
