이 항목의 내용
표준 편차 추정
군간/군내 공정 능력 분석은 다음 네 가지 표준 편차를 기반으로 합니다.
부분군 내부 표준 편차
σ군내는 부분군 내 변동의 추정치입니다(예: 한 교대조, 한 조작자 또는 하나의 원자재 배치). Minitab에서는 다음 방법 중 하나를 사용하여 σ군내를 추정합니다.
- 합동 표준 편차:
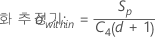
설명:
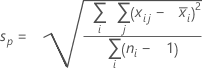
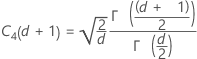
참고
기본 방법을 변경하고 불편화 상수를 사용하지 않을 경우 σ군내는 Sp로 추정됩니다.
용어 설명 d Sp= Σ (ni- 1)에 대한 자유도 Xij i번째 부분군의 j번째 관측치 X̅i i번째 부분군의 평균 ni i번째 부분군의 관측치 수 C4(d+1) 불편화 상수 Γ(·) 감마 함수 - 부분군 범위의 평균(Rbar):

설명:
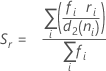
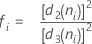
n이 모두 같은 경우:
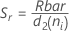
용어 설명 ri i번째 부분군의 범위 d2 (ni) 표에 있는 불편화 상수(자세한 내용은 불편화 상수 d2(), d3(), d4()에 대한 절 참조) d3 (ni) 표에 있는 불편화 상수(자세한 내용은 불편화 상수 d2(), d3(), d4()에 대한 절 참조) ni i번째 부분군의 관측치 수 - 부분군 표준 편차의 평균(Sbar):
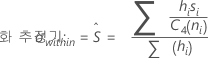
설명:
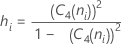
참고
기본 설정을 변경하고 불편화 상수를 사용하지 않을 경우 σ군내는 Σ Si / 부분군의 개수로 추정됩니다.
용어 설명 C4(ni) 불편화 상수(합동 표준 편차에 정의된 대로) Si 부분군 i의 표준 편차 ni i번째 부분군의 관측치 수
부분군 군간 표준 편차
σ군간은 부분군 간 변동의 추정치입니다(예: 설정된 간격, 배치 또는 여러 조작자에 의해 수집된 부분군).
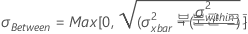
- 이동 범위[MR]의 평균:

설명:
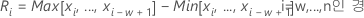
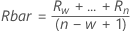
용어 설명 Ri i번째 이동 범위[MR] w 이동 범위[MR]에 사용되는 관측치 수. 기본값은 w = 2입니다. d2(w) 표에 있는 불편화 상수(자세한 내용은 불편화 상수 d2(), d3(), d4()에 대한 절 참조) - 이동 범위[MR]의 중위수:

설명:

용어 설명 MRi i번째 이동 범위[MR] 
MRi의 중위수 w 이동 범위[MR]에 사용되는 관측치 수. 기본값은 w = 2입니다. d4(w) 표에 있는 불편화 상수(자세한 내용은 불편화 상수 d2(), d3(), d4()에 대한 절 참조) - 연속 차이 제곱 평균(MSSD)의 제곱근:
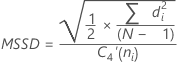
참고
기본 설정을 변경하고 불편화 상수를 사용하지 않을 경우 σ군내는 다음으로 추정됩니다.

용어 설명 di 연속 그룹 평균의 차이 C4(ni) 불편화 상수(합동 표준 편차에 정의된 대로) C4'(ni) 불편화 상수 ≈ c4(ni). 자세한 내용은 불편화 상수 c4'()에 대한 절을 참조하십시오. N 총 관측치 수 ni i번째 부분군의 관측치 수
군간/군내 표준 편차

| 용어 | 설명 |
|---|---|
| σ2군간 | 부분군 간 분산 |
| σ2군내 | 부분군 내 분산 |
전체 표준 편차

설명:
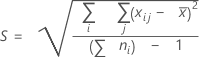
참고
기본적으로 Minitab에서는 σ전체를 추정할 때 불편화 상수를 사용하지 않습니다. σ전체는 S로 추정됩니다. 불편화 상수를 사용하여 전체 표준 편차를 추정하려면 공정 능력 분석을 수행할 때 추정치 하위 대화 상자에서 이 옵션을 변경할 수 있습니다. Minitab에서 항상 불편화 상수를 기본적으로 사용하도록 하려면 을 선택한 다음 적절한 옵션을 선택하십시오.
| 용어 | 설명 |
|---|---|
| Xij | i번째 부분군의 j번째 관측치 |
| X̅ | 공정 평균 |
| ni | i번째 부분군의 관측치 수 |
| C4 (N) | 불편화 상수(합동 표준 편차에 정의된 대로) |
| N(또는 Σ ni) | 총 관측치 수 |
Box-Cox 변환
Box-Cox 변환은 다음 표에 표시된 대로 표준화된 변환 변수의 표준 편차를 최소화하는 람다 값을 추정합니다. 결과 변환은 λ ҂ 0일 때 Yλ, λ = 0일 때 ln Y입니다.
Box-Cox 방법은 여러 유형의 변환을 검색합니다. 다음 표에는 Y'가 데이터 Y의 변환인 몇 가지 일반적인 변환이 나와 있습니다.
| 람다(λ) 값 | 변환 |
|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
