전체 공정 능력에 대한 Z.LSL, Z.USL 및 Z.Bench
전체 공정 능력에 대한 벤치마크 Z 통계량은 해당 통계량에 대한 표준 정규 (0, 1) 분포를 사용하여 Z 값을 찾음으로써 계산됩니다.
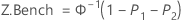
설명:
표기법
| 용어 | 설명 |
|---|---|
| Φ (X) | 표준 정규 분포의 누적 분포 함수(CDF) |
| Φ-1 (X) | 표준 정규 분포의 역 CDF |
 | 전체 표준 편차 |
규격 한계가 두 개인 공정의 Z.bench에 대한 신뢰 구간
양측 구간
설명
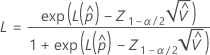
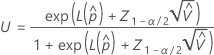
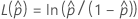
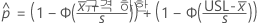
다음을 계산하려면 
, 에 대한 공식의 매개변수에 대한 표본 추정치를 대체합니다. 
:
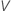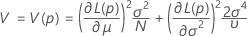
설명
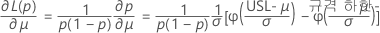
단측 신뢰 상한
단측 신뢰 상한을 계산하려면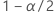 
에게 
U의 정의에서.
표기법
| 용어 | 설명 |
|---|---|
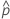 | 규격 한계를 벗어나는 추정 꼬리 확률 |
 | 표준 정규 분포의 (1 - α/2)번째 백분위수 |
| α | 신뢰 수준에 대한 알파 |
 | 공정 평균(표본 데이터 또는 과거 값에서 추정됨)공정 평균(표본 데이터 또는 과거 값에서 추정됨) |
| s | 부분군 내 표본 표준 편차 |
| υ | s에 대한 자유도 |
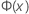 | 표준 정규 분포의 누적분포함수(CDF) |
 | 표준 정규 분포의 확률 밀도 함수(PDF) |
| 규격 상한 | 규격 상한 |
| 규격 하한 | 규격 하한 |
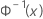 | 표준 정규 분포의 역 CDF |
규격 한계가 하나인 공정의 Z.bench에 대한 신뢰 구간
Z.Bench에 대한 신뢰 구간은 공정의 규격 한계에 따라 계산됩니다.
규격 하한, 양측 신뢰 구간
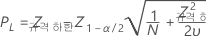
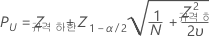
규격 하한, 단측 신뢰 한계
Minitab에서는 다음 방정식을 풀어 p1을 찾습니다.
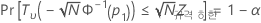
설명
규격 상한, 양측 신뢰 구간
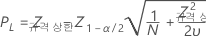
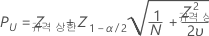
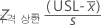
규격 상한, 단측 신뢰 한계
Minitab에서는 다음 방정식을 풀어 p2을 찾습니다.
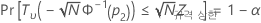
설명
표기법
| 용어 | 설명 |
|---|---|
| 규격 하한 | 규격 하한 |
| 규격 상한 | 규격 상한 |
| α | 신뢰 수준에 대한 알파 |
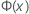 | 표준 정규 분포의 누적분포함수(CDF) |
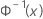 | 표준 정규 분포의 역 CDF |
 | 표준 정규 분포의 (1 - α/2)번째 백분위수 |
| N | 총 측정값 수 |
| υ | s에 대한 자유도 |
 | 공정 평균(표본 데이터 또는 과거 값에서 추정됨)공정 평균(표본 데이터 또는 과거 값에서 추정됨) |
| s | 표본 전체 표준 편차 |
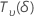 | 를 사용하여 비중심 T 분포로 분포되는 랜덤 변수  자유도와 비중심성 매개변수 δ |
