관측 성능에 대한 PPM < 규격 하한
백만 개 중에서 규격 하한보다 작은 측정값을 갖는 부품의 수는 다음과 같이 계산됩니다.

표기법
| 용어 | 설명 |
|---|---|
| 규격 하한 | 규격 하한 |
| N | 총 관측치 수 |
관측 성능에 대한 PPM > 규격 상한
백만 개 중에서 규격 상한보다 큰 측정값을 갖는 부품의 수는 다음과 같이 계산됩니다.

표기법
| 용어 | 설명 |
|---|---|
| 규격 상한 | 규격 상한 |
| N | 총 관측치 수 |
관측 성능에 대한 PPM 총계
백만 개의 부품 중에서 규격 한계를 벗어나는 총 부품 수는 다음과 같이 계산됩니다.

표기법
| 용어 | 설명 |
|---|---|
| 규격 하한 | 규격 하한 |
| 규격 상한 | 규격 상한 |
| N | 총 관측치 수 |
PPM 및 규격 이탈률(%)에 대한 신뢰 구간
신뢰 구간의 계산은 결과를 올바른 단위로 변환하는 마지막 단계를 제외하고 PPM 및 백분율에 대해 동일합니다. 다음 공식은 양측 100(1 –  )% 신뢰 구간. 단측 신뢰 구간을 찾으려면
)% 신뢰 구간. 단측 신뢰 구간을 찾으려면 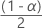 와 함께 (1 –
와 함께 (1 –  ).
).
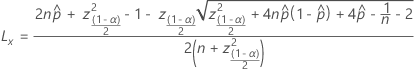
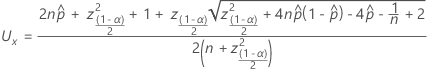
수식의 결과를 PPM으로 변환하려면 1,000,000을 곱합니다.
수식의 결과를 백분율로 변환하려면 100을 곱합니다.
관측치가 규격 한계를 벗어나는 단위가 없으면 신뢰 하한은 0입니다. 관측된 모든 단위가 규격 한계를 벗어나면 신뢰 상한은 1입니다.
표기법
| 용어 | 설명 |
|---|---|
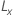 | 신뢰 하한 |
 | 신뢰 상한 |
| n | 전체 단위 수 |
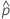 | 단위가 사양을 벗어난 경험적 확률: 불량 수 / 전체. |
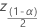 | (1 –  )/표준 정규 분포의 2 백분위수 )/표준 정규 분포의 2 백분위수 |
 | 1 – 신뢰 수준 |
참고 문헌
Newcombe, R. G. (1998). Two-sided confidence intervals for the single proportion: comparison of seven methods. Statistics in Medicine, 17(8), 857-872.
Tong, L. I., & Chen, J. P. (1998). Lower confidence limits of process capability indices for nonnormal process distributions. International Journal of Quality & Reliability Management, 15(8/9), 907-919.
