규격 하한
공정의 규격 하한(LSL)은 제품 또는 서비스에 대해 최소로 허용되는 값입니다. 이 한계는 공정이 어떻게 수행되고 있는 지가 아니라 공정이 어떻게 수행되어야 하는지 나타냅니다. LSL은 공정 능력 분석을 설정할 때 지정합니다.
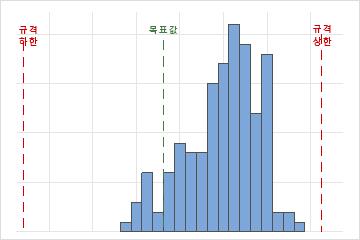
해석
고객 요구 사항을 정의하고 공정이 요구 사항을 충족하는 품목을 생산하는지 여부를 평가하려면 LSL 및 USL을 사용합니다.
규격 상한과 규격 하한은 히스토그램에 수직 파선으로 표시됩니다. 측정값이 규격 한계 내에 있는지 여부를 평가하려면 히스토그램 막대와 이 선을 비교하십시오.
규격 산포는 규격 상한과 규격 하한 간의 거리(USL – LSL)입니다. 한 회사에서 볼펜을 생산하고 볼의 목표 외경이 0.35mm라고 가정합니다. 볼 외경의 허용 범위는 0.34 - 0.36mm입니다. 따라서 LSL은 0.34, USL은 0.36, 규격 산포는 0.02mm입니다.
Minitab에서는 규격 산포를 공정 산포와 비교하여 공정 능력을 결정합니다.
목표값
목표값은 고객 요구 사항을 기준으로 하는 공정의 이상적인 값입니다. 예를 들어, 한 실린더 부품의 지름이 32mm일 때 제품이 최적의 성능을 제공한다면 이 부품의 목표값은 32mm입니다.
해석
고객 요구 사항을 정의하고 관측치와 비교하려면 목표값을 사용합니다.
목표값은 항상은 아니지만 일반적으로 대부분 규격 하한과 규격 상한의 중간에 위치합니다. 목표값이 있으면 공정의 중심이 목표값 가까이 있는지 여부를 조사하십시오.
규격 상한
공정의 규격 상한(USL)은 제품 또는 서비스에 대해 최대로 허용되는 값입니다. 이 한계는 공정이 어떻게 수행되고 있는 지가 아니라 공정이 어떻게 수행되어야 하는지 나타냅니다. USL은 공정 능력 분석을 설정할 때 지정합니다.

해석
고객 요구 사항을 정의하고 공정이 요구 사항을 충족하는 품목을 생산하는지 여부를 평가하려면 LSL 및 USL을 사용합니다.
규격 상한과 규격 하한은 히스토그램에 수직 파선으로 표시됩니다. 측정값이 규격 한계 내에 있는지 여부를 평가하려면 히스토그램 막대와 이 선을 비교하십시오.
규격 산포는 규격 상한과 규격 하한 간의 거리(USL – LSL)입니다. 한 회사에서 볼펜을 생산하고 볼의 목표 외경이 0.35mm라고 가정합니다. 볼 외경의 허용 범위는 0.34 - 0.36mm입니다. 따라서 LSL은 0.34, USL은 0.36, 규격 산포는 0.02mm입니다.
Minitab에서는 규격 산포를 공정 산포와 비교하여 공정 능력을 결정합니다.
표본 중위수
표본 중위수는 데이터 집합의 중간점입니다. 중간점 값은 관측치의 반이 이 값보다 크고 관측치의 반이 이 값보다 작은 점입니다. 중위수는 관측치에 순위를 매기고 순위가 [N + 1] / 2인 관측치를 찾는 방법으로 결정됩니다. 관측치의 수가 짝수이면 순위가 N / 2인 관측치와 순위가 [N / 2] + 1인 관측치의 평균 값이 중위수입니다.
해석
표본 중위수를 사용하여 공정의 중위수 값을 추정할 수 있습니다. 대부분의 데이터에서 중위수는 공정의 일반적인 데이터에 대한 적절한 추정치입니다. 일반적으로 중위수가 공정 목표값에 가까워지기를 원합니다.
종 모양의 대칭 분포를 따르는 데이터의 경우 표본 평균은 일반적으로 공정의 일반적인 데이터를 잘 추정합니다. 종 모양의 대칭 분포를 따르지 않는 데이터의 경우 표본 평균이 일반 데이터에서 멀리 떨어져 있는 경우가 있습니다. 표본 중위수는 평균이 일반 데이터와 멀리 떨어져 있을 때 일반적인 데이터를 더 잘 나타냅니다.
표본 평균
표본 평균은 표본 측정값의 평균입니다.
해석
공정의 평균 값을 추정하려면 표본 평균을 사용합니다. 일반적으로 평균이 공정 목표값에 가까워지기를 원합니다.
종 모양의 대칭 분포를 따르는 데이터의 경우 표본 평균은 일반적으로 공정의 일반적인 데이터를 잘 추정합니다. 종 모양의 대칭 분포를 따르지 않는 데이터의 경우 표본 평균이 일반 데이터에서 멀리 떨어져 있는 경우가 있습니다. 표본 중위수는 평균이 일반 데이터와 멀리 떨어져 있을 때 일반적인 데이터를 더 잘 나타냅니다.
표본 표준 편차
표본 표준 편차는 모든 측정값의 표준 편차이며 공정의 전체 변동에 대한 추정치입니다. 데이터가 제대로 수집된 경우 전체 표준 편차는 전체 변동의 모든 원인을 포착합니다. 이 경우에는 시간이 경과함에 따라 고객이 경험하는 공정의 실제 변동을 나타냅니다.
해석
표준 편차는 산포, 즉 데이터가 평균을 중심으로 퍼져 있는 정도를 나타내는 가장 일반적인 측도입니다. 표본 표준 편차가 클수록 데이터가 평균 주위로 더 넓게 퍼져 있다는 것을 나타냅니다. 일반적으로 동일한 공정은 표준 편차가 클 때보다 표준 편차가 작을 때 더 성능이 좋습니다.
표본 N
표본 크기(N)는 데이터에 포함된 전체 관측치 수입니다. 예를 들어, 크기가 5인 부분군을 20개 수집한 경우 표본 N은 100입니다.
해석
표본 크기를 평가하려면 N을 사용합니다.
일반적으로 표본 크기가 클수록 보다 신뢰할 수 있는 공정 능력 추정치를 얻을 수 있습니다. 일부 전문가는 공정 능력 분석에 총 100개 이상의 관측치를 사용할 것을 권장합니다.
