계량형 합격 표본 추출(생성/비교)에 대한 주요 결과 해석

계량형 합격 표본 추출 계획을 해석하려면 다음 단계를 수행하십시오.

이 항목의 내용

1단계: 표본 추출 계획의 표본 크기 및 합격 기준 결정

2단계: 대체 계획의 로트 합격 또는 불합격 확률 비교

1단계: 표본 추출 계획의 표본 크기 및 합격 기준 결정

합격 표본 추출 계획을 생성하는 경우 제품 로트에서 검사할 품목 수를 결정하고 표본 측정값을 기반으로 언제 데이터 로트를 합격 또는 불합격시킬 것인지 결정해야 합니다.

사용자가 지정한 로트 크기, AQL, RQL, 생산자의 위험(α), 소비자의 위험(β), 공정의 규격을 사용하여 Minitab에서는 특정 표본 크기 및 임계 거리로 적절한 표본 추출 계획을 결정합니다.

임계 거리는 로트의 합격 또는 불합격 여부를 결정하기 위해 Minitab이 표본 평균 및 규격 한계와 비교하는 데 사용하는 값입니다.

표본 측정값을 수집한 후 평균과 표준 편차에서 계산된 Z 값을 임계 거리와 비교하여 로트 전체를 합격시킬 것인지 불합격시킬 것인지 여부를 결정합니다.

로트 표준 편차가 최대 표준 편차(MSD)보다 작으면 (평균 – 규격 하한) / 표준 편차 ≥ 3.55750인 경우 로트 전체를 합격시켜야 합니다.

생성된 계획 표본 크기 104 임계 거리(k 값) 3.55750 Z.LSL = (평균 - 규격 하한)/과거 표준 편차 Z.LSL ≥ k인 경우 로트를 합격시키고 그렇지 않은 경우 불합격시킵니다.

주요 결과: 표본 크기, 임계 거리

이 결과에서 표본 크기는 104입니다. 제품의 전체 로트에서 104개의 품목을 표본으로 추출해야 합니다. Minitab에서는 규격 하한 0.09인치를 사용하여 임계 거리가 3.557인지 결정합니다.

참고

규격 상한이 있으면 이 기준을 고려할 뿐만 아니라 (규격 상한 – 평균) / 표준 편차 ≥ 3.55750인 경우에도 로트를 합격시켜야 합니다. 두 기준 모두 참이어야 하며, 그렇지 않으면 로트 전체를 불합격시켜야 합니다.

2단계: 대체 계획의 로트 합격 또는 불합격 확률 비교

합격 표본 추출 계획을 생성한 후 전체 표본 크기를 줄이기 위해 표본 크기 및 임계 거리를 변경할 수 있습니다.

표본 크기, 임계 거리 또는 둘 다를 변경하여 계획을 비교하고 합격 위험이 어떻게 달라지는지 확인할 수 있습니다.

계량형 합격 표본 추출 - 생성/비교

로트 품질(백만 번당 불량품 수)

방법 규격 하한(LSL) 0.09 과거 표준 편차 0.025 로트 크기 2500 합격 품질 수준(AQL) 100 불합격 품질 수준(RQL 또는 LTPD) 300

사용자 정의 계획 비교 백만 번당 표본 임계 불량품 크기(n) 거리(k) 수 합격 확률 기각 확률 AOQ ATI 50 3.5575 100 0.873 0.127 85.6 360.4 50 3.5575 300 0.187 0.813 54.9 2042.6 75 3.5575 100 0.919 0.081 89.1 271.3 75 3.5575 300 0.138 0.862 40.1 2165.8 100 3.5575 100 0.947 0.053 90.9 227.5 100 3.5575 300 0.104 0.896 30.0 2250.3 104 3.5575 100 0.950 0.050 91.1 223.2 104 3.5575 300 0.100 0.900 28.6 2261.3

평균 출검 품질 한계(AOQL) 표본 임계 백만 번당 크기 거리(k) AOQL 불량품 수 50 3.5575 96.8 148.3 75 3.5575 101.0 141.9 100 3.5575 104.2 140.1 104 3.5575 104.6 140.0 Z.LSL = (평균 - 규격 하한)/과거 표준 편차 Z.LSL ≥ k인 경우 로트를 합격시키고 그렇지 않은 경우 불합격시킵니다.

주요 결과: 합격 확률, 불합격 확률

표본 크기가 104이고 임계 거리가 3.5575인 계획이 AQL에서의 목표 α 위험 5% 및 RQL에서의 목표 β 위험 10%와 가장 일치합니다. 표본 크기를 100으로 약간 줄인 계획도 목표 위험 수준과 일치합니다.

표본 크기가 75개이고 임계 거리가 3.5575인 계획도 합격 위험이 있습니다. 그러나 표본 크기가 50이고 임계 거리가 3.5575이면 AQL(0.873)에서의 합격 확률이 너무 낮고 RQL(0.187)에서의 합격 확률이 너무 높습니다.

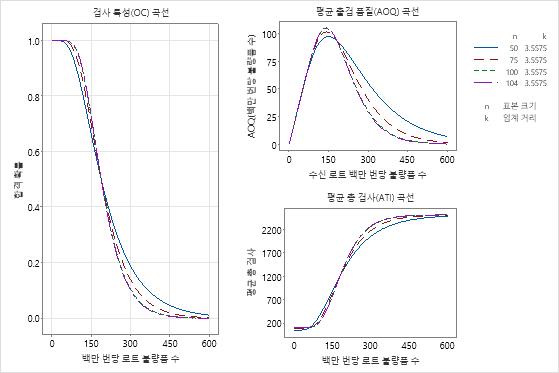
합격 표본 추출 계획 그래프는 표본 추출 계획을 시각적으로 비교하는 데 도움이 됩니다.

이 결과에서는 표본 크기를 104에서 100으로 줄이는 결정을 쉽게 내릴 수 있습니다. AQL 및 RQL에서의 합격 확률은 0.5%(0.95 – 0.947) 미만으로 변경됩니다. 표본 크기를 75로 줄이거나 분석을 다시 실행하고 75와 100 사이의 표본 크기를 선택할 수 있습니다.