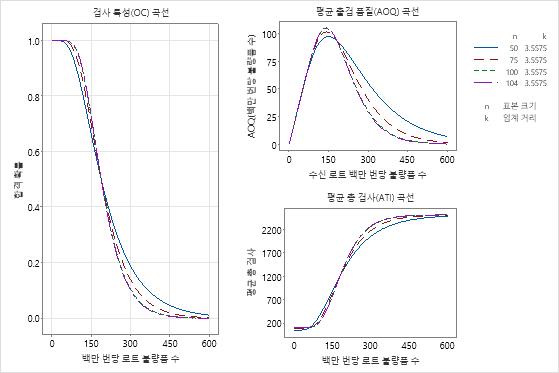
한 제조 엔지니어가 수입하는 2인치 파이프의 벽 두께를 확인하기 위해 계량형 표본 추출 계획을 구현했습니다. 파이프 벽 두께의 규격 하한은 0.09인치입니다. 엔지니어와 공급업체는 AQL이 백만개당 불량 수 100이고 RQL은 백만개당 불량 수 300임에 동의합니다. 이러한 규격을 기반으로 엔지니어는 2500개 파이프 로트당 104개의 파이프를 랜덤하게 선택하여 측정합니다. 계산된 Z-값이 임계 거리(3.55750)보다 큰 경우 엔지니어는 로트 전체를 합격시킵니다.
교대조 관리자는 104개의 파이프를 측정하는 데 너무 많은 시간이 걸린다는 점을 우려합니다. 관리자는 더 적은 수(예: 50개)의 파이프를 측정하고자 합니다. 엔지니어는 다른 표본 추출 계획을 조사하여 각 계획의 위험과 이점을 확인한다는 데 동의합니다.
- 을 선택합니다.
- 드롭다운 리스트에서 사용자 정의의 표본 추출 계획 비교을 선택합니다.
- 품질 수준의 단위에서 백만개당 불량 수을 선택합니다.
- 합격 품질 수준(AQL)에 100을 입력합니다.
- 불합격 품질 수준(RQL 또는 LTPD)에 300을 입력합니다.
- 표본 크기에 50 75 100 104를 입력합니다.
- 임계 거리(k 값)에 3.55750을 입력합니다.
- 규격 하한에 0.09를 입력합니다.
- 과거 표준 편차에 0.025를 입력합니다.
- 로트 크기에 2500을 입력합니다.
- 확인을(를) 클릭합니다.
결과 해석
엔지니어는 여러 표본 추출 계획의 그래프를 비교하고 표본 크기가 100인 표본 추출 계획과 104인 표본 추출 계획이 매우 유사하다는 것을 확인합니다. AQL 및 RQL에서의 합격 확률은 0.5%(0.95 – 0.947) 미만으로 변경됩니다. AOQ 변경과 ATI 변경도 매우 적습니다.
엔지니어는 또한 표본 크기가 50이면 품질 수준이 충분히 보호되지 않는다는 것을 확인합니다. 표본 크기가 50일 때 RQL(300 PPM)에서 로트의 합격 확률은 18.7%입니다. 또한 AQL(100 PPM)에서 합격시켜야 할 로트의 불합격 확률도 12.7%로, 생산자에게는 너무 높습니다.
엔지니어는 파이프 75개의 표본 추출 계획을 고려할 의사가 있습니다. 공급업체가 파이프 두께 변동성을 줄이는 데 동의할 경우 합격 확률의 위험은 적절한 것으로 보입니다. 엔지니어는 75와 100 사이의 다른 표본 크기를 조사하기로 결정합니다.
방법
| 규격 하한(LSL) | 0.09 |
|---|---|
| 과거 표준 편차 | 0.025 |
| 로트 크기 | 2500 |
| 합격 품질 수준(AQL) | 100 |
| 불합격 품질 수준(RQL 또는 LTPD) | 300 |
사용자 정의 계획 비교
| 표본 크기(n) | 임계 거리(k) | 백만 번당 불량품 수 | 합격 확률 | 기각 확률 | AOQ | ATI |
|---|---|---|---|---|---|---|
| 50 | 3.5575 | 100 | 0.873 | 0.127 | 85.6 | 360.4 |
| 50 | 3.5575 | 300 | 0.187 | 0.813 | 54.9 | 2042.6 |
| 75 | 3.5575 | 100 | 0.919 | 0.081 | 89.1 | 271.3 |
| 75 | 3.5575 | 300 | 0.138 | 0.862 | 40.1 | 2165.8 |
| 100 | 3.5575 | 100 | 0.947 | 0.053 | 90.9 | 227.5 |
| 100 | 3.5575 | 300 | 0.104 | 0.896 | 30.0 | 2250.3 |
| 104 | 3.5575 | 100 | 0.950 | 0.050 | 91.1 | 223.2 |
| 104 | 3.5575 | 300 | 0.100 | 0.900 | 28.6 | 2261.3 |
평균 출검 품질 한계(AOQL)
| 표본 크기 | 임계 거리(k) | AOQL | 백만 번당 불량품 수 |
|---|---|---|---|
| 50 | 3.5575 | 96.8 | 148.3 |
| 75 | 3.5575 | 101.0 | 141.9 |
| 100 | 3.5575 | 104.2 | 140.1 |
| 104 | 3.5575 | 104.6 | 140.0 |