표본 분포는 모집단의 랜덤 표본에서 가능한 통계 값을 얻을 수 있는 우도를 설명합니다 즉, 해당 크기의 모든 랜덤 표본 비율이 해당 값을 제공합니다. 부트스트래핑은 단일 랜덤 표본에서 복원으로 여러 표본을 가져와서 표본 추출 분포를 추정하는 방법입니다. 이렇게 반복된 표본을 재표본이라고합니다. 각 재표본은 원래 표본 크기와 같습니다.
원래 표본은 원래 표본이 그려진 모집단을 나타냅니다. 따라서 이 원래 표본의 재표본은 모집단에서 여러 표본을 가져올 경우 얻게 되는 것을 나타냅니다. 통계량의 부트스트랩 분포는 재표본을 기반으로 하며 통계량의 부트스트랩 분포를 나타냅니다.
예를 들어, 파란색 M&M의 모집단 표본 추출 분포를 추정하려고 합니다. 랜덤 패킷을 열고 102개의 M&M가 있고 그 중 23개(22.5%)가 파란색인지 확인합니다. 이 원래 표본에서 복원으로 반복된 표본 추출은 모집단이 어떻게 보일 수 있는지를 흉내냈습니다. 재표본을 가져오기 위해 원래 표본에서 M&M가 랜덤으로 선택되고 색상이 기록된 다음 M&M를 다시 표본에 놓습니다. 단일 재표본을 완료하려면 이 작업을 102번(원래 표본의 크기)하십시오. 다음 막대 차트는 원래 표본에서 가져온 단일 부트스트랩 표본을 나타냅니다.
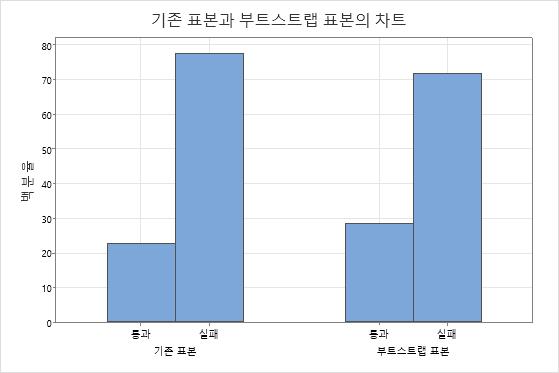
재표본은 복원으로 표본 추출하여 완료되었기 때문에 부트스트랩 표본 비율은 보통 원래 비율과 정확하게 일치하지 않습니다. 이 막대 차트는 원래 표본이 M&M의 약 22.5%가 파란색인 반면 부트스트랩 표본은 M&M의 약 28.4%가 파란색이었음을 보여줍니다. 부트스트랩 분포을 생성하려면 여러 재표본을 가져오십시오. 다음 히스토그램은 M&M의 원래 패킷의 1,000개의 재표본에 대한 부트스트랩 분포를 보여줍니다.
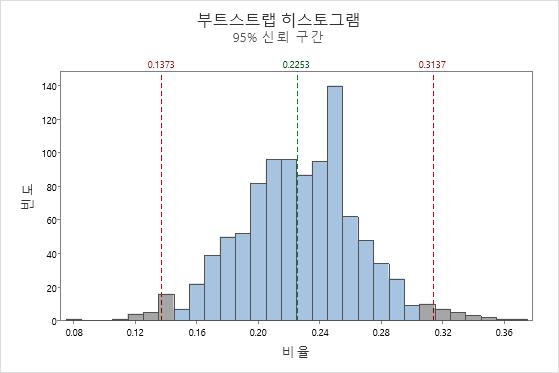
부트스트랩 분포는 약 22.5%에서 중심에 있습니다. 즉, 모집단 비율의 추정치입니다. 빨간색 기준선은 95%의 신뢰 구간을 나타냅니다. 부트스트래핑 분포 값의 중간 95%는 파란색 M&M의 모집단 비율에 대한 95% 신뢰 구간을 제공합니다. 이 예에서는 파란색 M&M의 모집단 비율이 대략 13.7%와 31.4% 사이에 있다고 95% 확신할 수 있습니다.
부트스트래핑 및 중심 극한 정리
중심 극한 정리는 확률 및 통계의 기초 정리입니다. 이 정리는 
, 즉 분산이 유한한 모집단에서 선택한 랜덤 표본의 평균의 분포는 모집단 분포의 모양에 관계없이, 표본 크기가 클 때 거의 정규 분포를 따르는 것을 말합니다. 부트스트래핑은 중심 극한 정리가 어떻게 작동하는지 쉽게 이해하는 데 사용할 수 있습니다. 지수 분포의 데이터를 고려합니다.
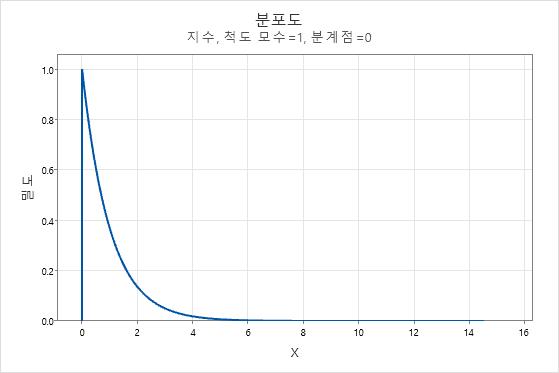
데이터는 정규 분포가 아님이 확실합니다. 하지만 이제 50개의 표본 관측치를 가져와서 10개의 재표본 평균에 대한 부트스트랩 분포를 생성할 것입니다.
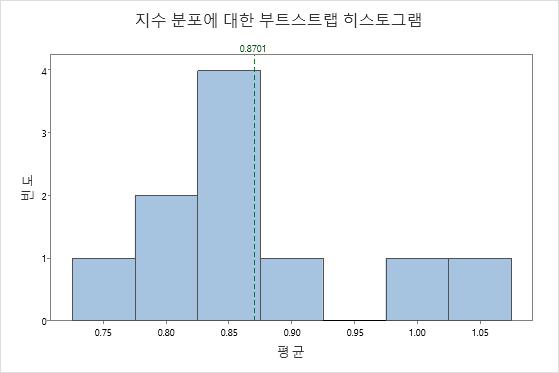
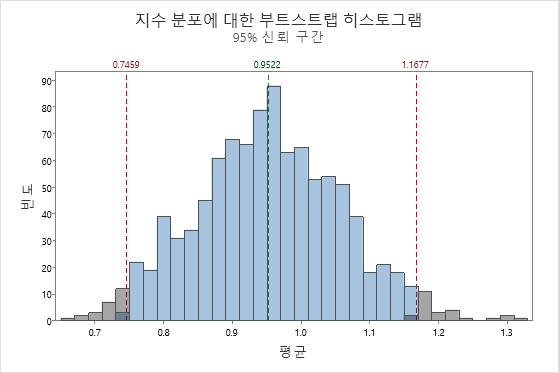
평규 분포는 지수 분포와 매우 다릅니다. 이는 정규 분포에 훨씬 더 가깝습니다. 이 유사성은 재표본 수가 증가할 때 증가합니다. 1,000개의 재표본이 있는 경우 재표본의 평균 분포는 대략 정규 분포입니다.
