Weibull 분포는 공학, 의학 연구, 품질 관리, 재무 및 기상학 분야의 광범위한 응용 부문을 모형화할 수 있는 다용도 분포입니다. 예를 들어, 이 분포는 신뢰도 분석과 함께 수명 데이터를 모형화하기 위해 자주 사용됩니다. Weibull 분포는 공정 능력 분석에서 치우친 공정 데이터를 모형화하는 데도 사용됩니다.
Weibull 분포는 형상, 척도 및 분계점 모수를 사용하여 설명되며 3-모수 Weibull 분포로도 알려져 있습니다. 분계점 모수가 0인 경우 2-모수 Weibull 분포라고 합니다. 2-모수 Weibull 분포는 양수 변수에 대해서만 정의됩니다. 3-모수 Weibull 분포에는 0 및 음수 데이터도 사용할 수 있지만, 2-모수 Weibull 분포의 경우 모든 데이터가 0보다 커야 합니다.
모수들의 값에 따라 Weibull 분포는 여러 가지 형태를 가질 수 있습니다.
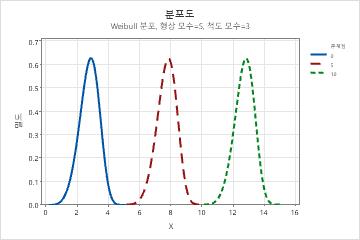
- 형상 모수의 효과
- 형상 모수는 데이터가 어떻게 분포되어 있는지 설명합니다. 형상이 3이면 정규 분포 곡선을 대략적으로 비슷하게 나타냅니다. 형상 값이 낮으면(1) 오른쪽으로 치우친 곡선을 나타냅니다. 형상 값이 높으면(10) 왼쪽으로 치우친 곡선을 나타냅니다.
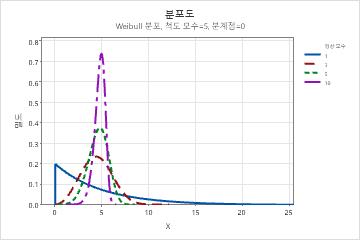
- 척도 모수의 효과
- 척도 또는 특성 수명은 데이터의 63.2 백분위수입니다. 척도는 Weibull 곡선의 분계점에 상대적인 위치를 정의하는 데, 이것은 평균이 정규 곡선의 위치를 정의하는 방식과 유사합니다. 척도는 Weibull 곡선의 분계점에 상대적인 위치를 정의하는 데 이것은 평균이 정규 곡선의 위치를 정의하는 방식과 유사합니다. 예를 들어 척도 20은 분계점 시간 후 처음 20시간 동안에는 장비의 63.2%에 고장이 발생한다는 것을 나타냅니다.
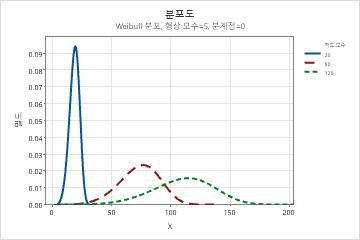
- 분계점 모수의 효과
- 분계점 모수는 0으로부터의 분포 이동을 설명합니다. 분계점이 음수이면 분포가 왼쪽으로 이동하며 분계점이 양수이면 분포가 오른쪽으로 이동합니다. 모든 데이터는 분계점보다 커야 합니다. 2-모수 Weibull 분포는 분계점이 0인 3-모수 Weibull 분포와 같습니다. 예를 들어, 3-모수 Weibull(3,100, 50) 분포의 형상과 산포는 2-모수 Weibull 분포(3, 100)와 같지만, 오른쪽으로 50 단위 이동합니다.