역 누적분포함수를 사용하여 보증 기간을 확인하는 예
예를 들어 한 가전 제품 제조업체에서 토스터 내부 가열 부품의 수명을 조사한다고 가정합니다. 특정 비율의 가열 부품에 고장이 발생하는 시간을 확인하여 보증 기간을 정하려고 합니다. 가열 부품의 고장 발생 시간은 평균이 1000시간이고 표준 편차가 300시간인 정규 분포를 따릅니다. 확률밀도함수(PDF)는 고장 확률이 더 높거나 더 낮은 영역을 식별하는 데 도움이 됩니다. 역 CDF는 각 누적 확률에 해당하는 고장 시간 값을 제공합니다.
역 CDF를 사용하면 가열 부품의 5%가 고장나는 시간, 모든 가열 부품의 95%가 고장나는 시간, 가열 부품의 5%만이 남아 있는 시간 등을 추정할 수 있습니다. 특정 누적 확률에 대한 역 CDF는 확률 밀도 함수 곡선 아래의 음영 영역 오른쪽에 있는 고장 시간과 같습니다.
5%가 고장 날 시간 확인
- 을(를) 선택합니다.
- 역 누적 확률을 선택합니다. 평균에 1000을 입력합니다. 표준 편차에 300을 입력합니다. 입력 상수에 0.05을 입력합니다.
- 확인을 클릭합니다.
가열 부품의 5%가 고장날 것으로 예상되는 시간은 0.05의 역 CDF 또는 506.544시간입니다.
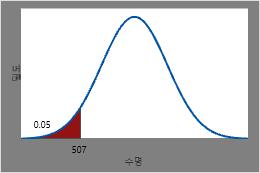
이 그림은 역 CDF를 보여줍니다.
95%가 고장 날 시간 확인
- 을(를) 선택합니다.
- 역 누적 확률을 선택합니다. 평균에 1000을 입력합니다. 표준 편차에 300을 입력합니다. 입력 상수에 0.025을 입력합니다. 확인을 클릭합니다.
가열 부품의 2.5%가 고장날 것으로 예상되는 시간은 0.025의 역 CDF 또는 412시간입니다.
- 2단계를 반복하고 0.975를 0.025 대신 입력합니다. 확인을 클릭합니다.가열 부품의 97.5%가 고장날 것으로 예상되는 시간은 0.975의 역 CDF 또는 1588시간입니다.
따라서 모든 가열 부품의 95%가 고장날 것으로 예상되는 시간은 0.025의 역 CDF와 0.975의 역 CDF이거나 412시간과 1588시간입니다.
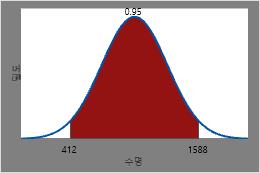
이 그림은 역 CDF를 보여줍니다.
5%의 수명이 남아 있는 시간 확인
- 을(를) 선택합니다.
- 역 누적 확률을 선택합니다. 평균에 1000을 입력합니다. 표준 편차에 300을 입력합니다. 입력 상수에 0.95을 입력합니다.
- 확인을 클릭합니다.
가열 부품의 5%만이 남아 있을 것으로 예상되는 시간은 0.95의 역 CDF 또는 1493시간입니다.
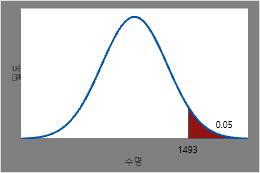
이 그림은 역 CDF를 보여줍니다.
CDF와 역 CDF를 초기하 분포와 함께 사용하는 예
이산형 분포의 역 누적 확률을 확인할 때 결과에는 열 집합 2개가 포함됩니다.
비율 p의 역 누적 확률이 있다고 가정할 때 결과의 첫 번째 열 집합에는 P(X ≤ x) ≤ p인 최대 x가 나열됩니다. 두 번째 열 집합에는 P(X ≤ x) ≥ p인 최소 x가 나열됩니다.
초기하 분포의 누적 확률 계산
- 워크시트의 C1 열에 0 1 2를 입력합니다.
C1 0 1 2 - 을(를) 선택합니다.
- 누적 확률을 선택합니다.
- 에서 모집단 크기(N)유형 20000.
- 에서 모집단 내 사건 카운트(M)유형 2000.
- 에서 표본 크기(n)유형 20.
- 선택 입력 열 해서 C1을 입력하세요. 확인을 클릭합니다.
누적분포함수
- P(X ≤ 0) = 0.121448. 결함이 하나도 발생하지 않을 확률은 약 12%입니다.
- P(X ≤ 1) = 0.391619. 결함이 0개나 1개 발생할 확률은 약 39%입니다.
- P(X ≤ 2) = 0.676941. 결함이 0개, 1개 또는 2개 발생할 확률은 약 68%입니다.
초기하 분포의 역 누적 확률 계산
이제 결함의 수와 관련된 누적 확률을 알게 되었으므로, 역 누적 확률을 계산할 수 있습니다.
누적 확률 p가 0.50인 결점의 수 x를 계산하려고 한다고 가정합니다. 이전 결과에서 P(X ≤ 1 ) = 0.391619 및 P(X ≤ 2 ) = 0.676941이라는 것을 알 수 있습니다. 초기하학적 분포는 이산적 분포이기 때문에 결함 수가 1과 2 사이일 수 없다. 즉, 결함이 1개나 2개일 수는 있지만, 1.4개는 아닙니다. 따라서 0.50을 선택하고 입력 상수 입력하면, Minitab은 출력 확률 두 가지를 모두 계산합니다. 다음 예시에서 확인할 수 있습니다:
- 을(를) 선택합니다.
- 역 누적 확률을 선택합니다.
- 에서 모집단 크기(N)유형 20000.
- 에서 모집단 내 사건 카운트(M)유형 2000.
- 에서 표본 크기(n)유형 20.
- 를 선택하고 입력 상수0.50을 입력하세요. 확인을 클릭합니다.
역 누적분포함수
첫 번째 확률은 x의 값을 나타내며, P(X ≤ x) < p and the second probability indicates the smallest x such that P(X ≤ x) ≥ p. In this example, the first probability shows the largest number of defectives, x = 2, such that P(X ≤ 2) <0.5 and the 2nd 가 결함 수인 x = 3을 나타내므로, P(X ≤ 3) ≥ 0.5가 된다.
역 CDF를 사용한 임계값 계산
표에서 찾는 대신 Minitab을 사용하여 가설 검정의 임계값을 계산할 수 있습니다.
α=0.02이고 자유도가 12인 카이-제곱 검정을 수행한다고 가정합니다. 해당 임계값은 무엇입니까? α=0.02는 누적 확률 값 1 - 0.02 = 0.98에 해당합니다.
- 을(를) 선택합니다.
- 역 누적 확률을 선택합니다.
- 자유도에 12을 입력합니다.
- 0.98을 선택하고 입력 상수 입력하세요.
- 확인을 클릭합니다.
임계값인 24.054가 표시됩니다. 카이-제곱 검정에서 검정 통계량이 임계값보다 크면 귀무 가설을 기각할 통계적 근거가 있다고 할 수 있습니다.
참고
이 예에서는 카이-제곱 분포를 사용합니다. 그러나 선택한 모든 분포에 대해 이와 동일한 단계를 수행합니다.
