이 항목의 내용
계량형 분포의 정의
계량형 분포는 계량형 랜덤 변수가 가질 수 있는 값의 확률을 나타냅니다. 계량형 랜덤 변수는 무한하고 셀 수 없는 가능한 값들의 집합(범위)을 갖는 랜덤 변수입니다.
계량형 랜덤 변수(X)의 확률은 변수의 PDF 곡선 아래의 면적으로 정의됩니다. 따라서 값의 범위만 0이 아닌 확률을 가질 수 있습니다. 계량형 랜덤 변수가 어떤 값과 같을 확률은 항상 0입니다.
몸무게 분포의 예
계량형 정규 분포로 성인 남성의 체중 분포를 나타낼 수 있습니다. 예를 들어, 한 남성의 체중이 160파운드와 170파운드 사이일 확률을 계산할 수 있습니다.
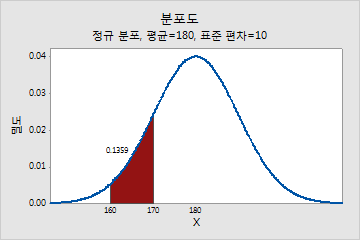
성인 남성의 체중 분포도
이 예에서 곡선 아래 음영 영역은 160파운드와 170파운드 사이의 범위를 나타냅니다. 이 범위의 면적은 0.136이므로, 랜덤하게 선택된 한 남성의 체중이 160파운드와 170파운드 사이일 확률은 13.6%입니다. 곡선 아래의 전체 면적은 1.0과 같습니다.
그러나 X가 어떤 값과 정확하게 같을 확률은 항상 0입니다. 한 점에서 곡선 아래 부분의 면적은 너비가 없어서 0이기 때문입니다. 예를 들어, 한 남성의 체중이 정확하게 190파운드일 확률은 0입니다. 체중이 190파운드를 넘거나 190파운드 미만이거나, 189.9파운드와 190.1파운드 사이일 확률은 0이 아닌 값으로 계산할 수 있지만, 정확하게 190파운드일 확률은 0입니다.
이산형 분포의 정의
이산형 분포는 이산형 랜덤 변수의 각 값이 발생할 확률을 나타냅니다. 이산형 랜덤 변수는 음수가 아닌 정수 리스트와 같이 셀 수 있는 값을 갖는 랜덤 변수입니다.
이산형 확률 분포를 사용하는 경우 이산형 랜덤 변수의 가능한 각 값이 0이 아닌 확률과 관련됩니다. 따라서 이산형 확률 분포는 보통 표 형식으로 표시됩니다.
고객 불만 수의 예
| x | P (X = x) |
|---|---|
| 5 | 0.037833 |
| 10 | 0.12511 |
| 15 | 0.034718 |
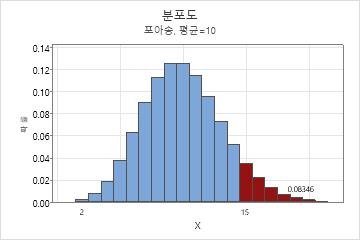
고객 불만 수의 분포도
이 예에서 음영 막대는 1일 고객 불만 수가 15개 이상일 때 발생 횟수를 나타냅니다. 막대 높이의 합은 0.08346이므로, 1일 통화 수가 15개 이상일 확률은 8.35%입니다.
