원하는 방법 또는 공식을 선택하십시오.
평균
숫자 묶음의 중심을 측정하는 데 가장 일반적으로 사용되는 측도. 모든 관측치의 합을 (비결측) 관측치 수로 나눈 값입니다.
공식
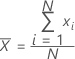
표기법
| 용어 | 설명 |
|---|---|
| xi | i번째 관측치 |
| N | 비결측 관측치 수 |
표준 편차
표본 표준 편차는 데이터 산포의 측도를 제공하며, 표본 분산의 제곱근과 같습니다.
공식
열에 x 1, x 2,..., x N이 포함되어 있고 평균이  이면 표본의 표준 편차는 다음과 같습니다.
이면 표본의 표준 편차는 다음과 같습니다.
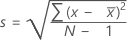
 이면 표본의 표준 편차는 다음과 같습니다.
이면 표본의 표준 편차는 다음과 같습니다.
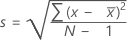
표기법
| 용어 | 설명 |
|---|---|
| x i | i번째 관측치 |
 | 관측치의 평균 |
| N | 비결측 관측치 수 |
분산
분산은 데이터가 평균 주위에 분산된 정도를 측정합니다. 분산은 표준 편차의 제곱과 같습니다.
공식
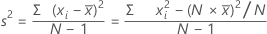
표기법
| 용어 | 설명 |
|---|---|
| xi | i번째 관측치 |
 | 관측치의 평균 |
| N | 비결측 관측치 수 |
합
공식

표기법
| 용어 | 설명 |
|---|---|
| xi | i번째 관측치 |
최소값
데이터 집합에서 가장 작은 값입니다.
중위수
표본 중위수는 데이터의 중간에 있습니다. 절반 이상의 관측치가 표본 중위수보다 작거나 같고 절반 이상의 관측치는 표본 중위수보다 크거나 같습니다.
값이 N개 포함된 열이 있다고 가정합니다. 중위수를 계산하려면 먼저 데이터를 가장 작은 값에서 가장 큰 값 순으로 정렬하십시오. N이 홀수이면 표본 중위수는 중간에 있는 값입니다. N이 짝수이면 표본 중위수는 중간에 있는 두 값의 평균입니다.
예를 들어, N = 5이고 데이터 x1, x2, x3, x4, x5가 있는 경우 중위수 = x3입니다.
N = 6이고 순서가 있는 데이터 x1, x2, x3, x4, x5, x6이 있는 경우:

여기서 x3과 x4는 세 번째와 네 번째 관측치입니다.
최대값
데이터 집합에서 가장 큰 값입니다.
평균
공식
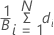
표기법
| 용어 | 설명 |
|---|---|
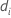 | i번째 재표본의 평균의 차이 |
| B | 재표본 수 |
| N | 원래 표본의 한 그룹의 관측치의 수 |
부트스트래핑 분포의 표준 편차
공식

표기법
| 용어 | 설명 |
|---|---|
 | 재표본의 차이의 평균 |
| B | 재표본 수 |
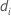 | i번째 재표본의 평균의 차이 |
p-값
공식
p-값은 대립 가설에 따라 다르게 계산됩니다.
- 평균이 귀무 가설에서의 값보다 작음:
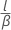
- 평균이 귀무 가설에서의 값과 같지 않음:
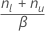
- 평균이 귀무 가설에서의 값보다 큼:

표기법
| 용어 | 설명 |
|---|---|
| l | d보다 작거나 같은 평균의 부트스트랩 차이의 수 |
| u | d보다 크거나 같은 평균의 부트스트랩 차이의 수 |
| β | 재표본 수 |
| nl | −d보다 작거나 같은 평균의 부트스트랩 차이의 수 |
| nu | d보다 작거나 같은 평균의 부트스트랩 차이의 수 |
| d | 평균의 표본 차이 |
