이 항목의 내용
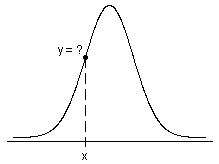
확률밀도함수
- 계량형 분포의 경우 X의 값이 구간 (a, b)에 포함될 확률은 정확히 구간 (a, b)에서 PDF 아래 영역입니다.
- 이산형 분포의 경우 X의 값이 구간 (a, b)에 포함될 확률은 정확히 (a, b)에서 가능한 이산형 값의 PDF(확률질량함수라고도 함)의 합입니다.
누적분포함수
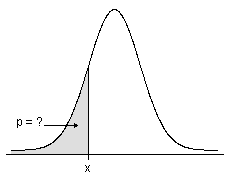
- 계량형 분포의 경우, CDF는 지정된 x-값에 대한 확률밀도함수 아래 영역을 제공합니다.
- 이산형 변수의 경우 CDF는 지정된 x-값에 대한 누적 확률을 제공합니다.
역 누적 확률
폐쇄된 구간 [0,1]의 숫자 p에 대해 랜덤 변수 X의 역 누적분포함수(ICDF)는 가능한 경우 X ≤ x일 확률이 p보다 크거나 같은 값 x를 나타냅니다.
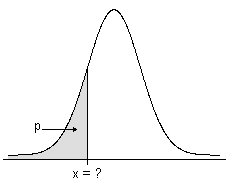
- 계량형 분포에 대한 ICDF
-
ICDF는 확률밀도함수 아래 영역과 연관된 값입니다. ICDF는 값과 연관된 영역인 누적분포함수(CDF)의 역입니다.
모든 계량형 분포의 경우 ICDF가 존재하며 0 < p < 1인 경우 고유합니다.
- 확률밀도함수(PDF)가 전체 실수 선에 대해 양수인 경우(예: 정규 PDF) p = 0 또는 p = 1에 대해 ICDF가 정의되지 않습니다.
- PDF가 특정 값보다 큰 모든 값에 대해 양수인 경우(예: 카이-제곱 PDF) p = 0에 대해서는 ICDF가 정의되지만 p = 1에 대해서는 정의되지 않습니다.
- PDF가 한 구간에서만 양수인 경우(예: 균등 PDF) p = 0 및 p = 1에 대해 ICDF가 정의됩니다.
- ICDF가 정의되어 있지 않으면 Minitab은 결측값(*)을 결과로 반환합니다.
- 이산형 분포에 대한 ICDF
- 이산형 분포에 대한 ICDF는 연속형 분포의 경우보다 더 복잡합니다. 예를 들어 n = 5, p = 0.4인 이항 분포에 대한 CDF를 계산하는 경우 CDF가 0.5인 x 값이 없습니다. x = 1인 경우 CDF는 0.3370입니다. x = 2인 경우 CDF가 0.6826로 증가합니다.
베타 분포
베타 분포는 보통 자연 하한 및 상한을 갖는 공정을 나타내기 위해 사용됩니다.
공식
확률밀도함수(PDF)는 다음과 같습니다.

표기법
| 용어 | 설명 |
|---|---|
| α | 형상 모수 1 |
| β | 형상 모수 2 |
| Γ | 감마 함수 |
| a | 하한 |
| b | 상한 |
a = 0, b = 1인 경우,
PDF는 다음과 같습니다.
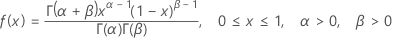


이항 분포
이항 분포는 n번의 독립 시행에서 발생하는 사건의 수를 나타내기 위해 사용됩니다. 가능한 값은 0과 n 사이의 정수입니다.
공식
평균 = np
분산 = np(1 – p)
확률질량함수(PMF)는 다음과 같습니다.
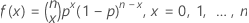
설명  는
는  와 같습니다.
와 같습니다.
일반적으로 k!는 다음과 같이 계산할 수 있습니다. 
표기법
| 용어 | 설명 |
|---|---|
| n | 시행 횟수 |
| x | 사건 발생 횟수 |
| p | 사건 확률 |
Cauchy 분포
Cauchy 분포는 0을 중심으로 대칭이지만 꼬리는 정규 분포의 꼬리보다 0에 천천히 근접합니다.
공식
확률밀도함수(PDF)는 다음과 같습니다.
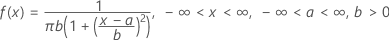
표기법
| 용어 | 설명 |
|---|---|
| a | 위치 모수 |
| b | 척도 모수 |
| π | Pi (~3.142) |
참고
값을 지정하지 않으면 a = 0 및 b = 1이 사용됩니다.
카이-제곱 분포
X가 표준 정규 분포를 따르면 X2은 자유도가 1인 카이-제곱 분포를 따르며 일반적인 표본 추출 분포로 사용할 수 있습니다.
n개의 독립적인 X2 변수의 합은 (여기서 X는 표준 정규 분포를 따름) 자유도가 n인 카이-제곱 분포를 따릅니다. 카이-제곱 분포의 모양은 자유도에 따라 다릅니다.
공식
확률밀도함수(PDF)는 다음과 같습니다.
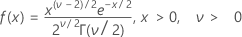
평균 = v
분산 = 2v
표기법
| 용어 | 설명 |
|---|---|
| ν | 자유도 |
| Γ | 감마 함수 |
| e | 자연 로그의 밑 |
이산형 분포
이산형 분포는 사용자에 의해 정의된 분포입니다. 예를 들어, 각각 0.2, 0.5 및 0.3의 확률을 갖는 세 개의 값 -1, 0 및 1로 구성된 분포에 관심이 있다고 가정합니다. 워크시트 열에 값을 입력하는 경우 이 열을 사용하여 랜덤 데이터를 생성하거나 확률을 계산할 수 있습니다.
| 값 | 확률 |
|---|---|
| −1 | 0.2 |
| 0 | 0.5 |
| 1 | 0.3 |
지수 분포
지수 분포는 단위의 순간 고장률(위험 함수)이 일정할 때 고장 사이의 시간을 모형화하기 위해 사용할 수 있습니다. 지수 분포는 Weibull 분포 및 감마 분포의 특별한 경우입니다.
공식
확률밀도함수(PDF)는 다음과 같습니다.
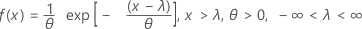
누적분포함수(CDF)는 다음과 같습니다.

평균 = θ + λ
분산 = θ2
표기법
| 용어 | 설명 |
|---|---|
| θ | 척도 모수 |
| λ | 분계점 모수 |
| exp | 자연 로그의 밑 |
참고
일부 참고 문헌에서는 모수에 1 / θ을 사용합니다.
F-분포
F-분포는 분산-비율 분포라고도 하며 분자 자유도와 분모 자유도의 두 가지 유형의 자유도가 있습니다. F-분포는 카이-제곱 분포를 따르는 독립적인 두 랜덤 변수를 각각 자유도로 나눈 값의 비율 분포입니다.
공식
확률밀도함수(PDF)는 다음과 같습니다.
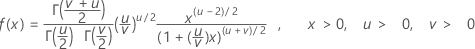

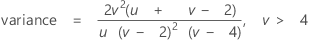
표기법
| 용어 | 설명 |
|---|---|
| Γ | 감마 함수 |
| u | 분자 자유도 |
| v | 분모 자유도 |
감마 분포
감마 분포는 양의 방향으로 치우친 데이터를 모형화하는 데 자주 사용됩니다.
공식
확률밀도함수(PDF)는 다음과 같습니다.

평균 = ab + θ
분산 = ab2
표기법
| 용어 | 설명 |
|---|---|
| a | 형상 모수(a = 1인 경우 감마 PDF는 지수 PDF와 같습니다.) |
| b | 척도 모수 |
| θ | 분계점 모수 |
| Γ | 감마 함수 |
| e | 자연 로그의 밑 |
참고
일부 참고 문헌에서는 모수에 1/ b을 사용합니다.
기하 분포
이산형 기하 분포는 확률이 p인 관심의 대상이 되는 사건이 포함된 일련의 독립적인 Bernoulli 실험에 적용됩니다.
공식
랜덤 변수 X가 확률이 p인 하나의 사건을 생성하기 위해 필요한 총 시행 횟수인 경우 X의 확률질량함수(PMF)는 다음과 같이 계산됩니다.

그리고 X는 다음과 같은 특성을 나타냅니다.
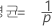
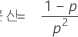
랜덤 변수 Y가 확률이 p인 첫 번째 사건이 관측되기 전에 발생하는 비사건의 개수인 경우 Y의 확률질량함수(PMF)는 다음과 같이 계산됩니다.

그리고 Y는 다음과 같은 특성을 나타냅니다.

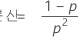
표기법
| 용어 | 설명 |
|---|---|
| X | 하나의 사건을 만들어내는 데 필요한 시행 횟수 Y + 1 |
| Y | 첫 번째 사건 전에 발생하는 비사건의 개수 |
| p | 각 시행에서 사건이 발생할 확률 |
초기하 분포
초기하 분포는 작은 모집단에서 비복원으로 추출되는 표본에 사용됩니다. 예를 들어, N대의 텔레비전이 배송되었는데, N1대는 양호(성공)하고 N2대는 불량(실패)입니다. N대 중 n대를 비복원으로 랜덤하게 추출하는 경우, n대 중 정확히 x대가 양호할 확률을 확인할 수 있습니다.
공식
확률질량함수(PMF)는 다음과 같습니다.
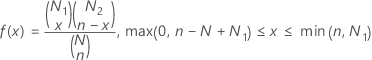


표기법
| 용어 | 설명 |
|---|---|
| N | N1 + N2 = 모집단 크기 |
| N1 | 모집단 내 사건 수 |
| N2 | 모집단 내 비사건 수 |
| n | 표본 크기 |
| x | 표본의 사건 수 |
정수 분포
정수 분포는 정수 집합에 대한 이산형 균등 분포입니다. 각 정수의 발생 확률은 모두 같습니다.
정규 분포
정규 분포(가우스 분포라고도 함)는 많은 물리학, 생물학 및 사회학적인 공정을 모형화할 수 있기 때문에 가장 많이 사용되는 통계 분포입니다.
공식
확률밀도함수(PDF)는 다음과 같습니다.
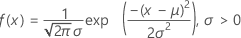
누적분포함수(CDF)는 다음과 같습니다.
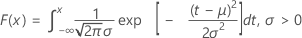
평균 = μ
분산 = σ 2
표준 편차 = σ
표기법
| 용어 | 설명 |
|---|---|
| exp | 자연 로그의 밑 |
| π | Pi (~3.142) |
Laplace 분포
Laplace 분포는 정규 분포보다 봉우리가 더 뾰족한 경우에 사용됩니다.
공식
확률밀도함수(PDF)는 다음과 같습니다.
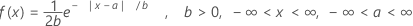
평균 = a
분산 = 2b2
표기법
| 용어 | 설명 |
|---|---|
| a | 위치 모수 |
| b | 척도 모수 |
| e | 자연 로그의 밑 |
최대 극단값 분포
분포의 가장 큰 값을 모형화하려면 최대 극단값 분포를 사용합니다. 여러 지수 분포가 있고 X(n)이 처음 n개의 최대값인 경우 X(n) – ln(n)은 최대 극단값 분포로 수렴합니다. 따라서 n 값이 큰 경우 최대 극단값은 X(n) – ln(n)과 매우 근사합니다.
공식
확률밀도함수(PDF)는 다음과 같습니다.

누적분포함수(CDF)는 다음과 같습니다.

평균 = μ + γσ
분산 = π 2 σ 2 / 6
표기법
| 용어 | 설명 |
|---|---|
| σ | 척도 모수 |
| μ | 위치 모수 |
| γ | Euler 상수(~0.57722) |
로지스틱 분포
대칭적이고 정규 분포와 비슷하지만 꼬리 부분이 더 두꺼운 계량형 분포입니다.
공식
확률밀도함수(PDF)는 다음과 같습니다.
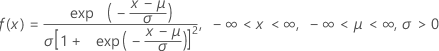
누적분포함수(CDF)는 다음과 같습니다.
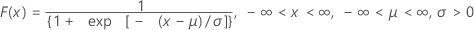
평균 = μ
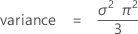
표기법
| 용어 | 설명 |
|---|---|
| μ | 위치 모수 |
| σ | 척도 모수 |
로그 로지스틱 분포
Y = log (x – λ)가 로지스틱 분포를 따르면 변수 x는 분계점이 λ인 로그 로지스틱 분포를 따릅니다.
공식
확률밀도함수(PDF)는 다음과 같습니다.
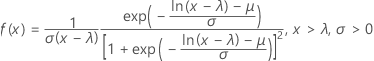
누적분포함수(CDF)는 다음과 같습니다.

σ < 1인 경우:

σ < 1/2인 경우:
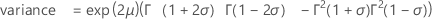
표기법
| 용어 | 설명 |
|---|---|
| μ | 위치 모수 |
| σ | 척도 모수 |
| λ | 분계점 모수 |
| Γ | 감마 함수 |
| exp | 자연 로그의 밑 |
로그 정규 분포
log(x – λ)가 정규 분포를 따르는 경우 변수 x는 로그 정규 분포를 따릅니다.
공식
확률밀도함수(PDF)는 다음과 같습니다.

누적분포함수(CDF)는 다음과 같습니다.



표기법
| 용어 | 설명 |
|---|---|
| μ | 위치 모수 |
| σ | 척도 모수 |
| λ | 분계점 모수 |
| π | Pi (~3.142) |
음이항 분포
이산형 음이항 분포는 확률이 p인 관심의 대상이 되는이벤트가 포함된 일련의 독립적인 Bernoulli 실험에 적용됩니다.
공식
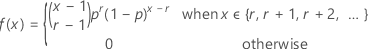

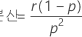
랜덤 변수 Y가 각각의 확률이 p인 r개의 사건을 관측하기 전에 발생하는 비사건의 개수인 경우, Y의 확률질량함수(PMF)는 다음과 같이 계산됩니다.
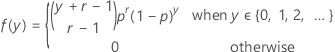
그리고 Y는 다음과 같은 속성을 나타냅니다.

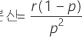
참고
이 음이항 분포는 Pascal 분포로도 알려져 있습니다.
표기법
| 용어 | 설명 |
|---|---|
| X | Y + r |
| r | 사건 발생 횟수 |
| p | 사건 확률 |
포아송 분포
포아송 분포는 일정한 발생률을 기반으로 사건의 수를 모형화하는 이산형 분포입니다. 포아송 분포는 독립 시행의 수가 크고 성공 확률이 작은 경우 이항 분포의 근사로 사용될 수 있습니다.
공식
확률질량함수(PMF)는 다음과 같습니다.
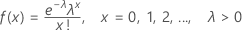
평균 = λ
분산 = λ
표기법
| 용어 | 설명 |
|---|---|
| e | 자연 로그의 밑 |
최소 극단값 분포
분포의 가장 작은 값을 모형화하려면 최소 극단값 분포를 사용합니다. Y가 Weibull 분포를 따르면 log(Y)는 최소 극단값 분포를 따릅니다.
공식
확률밀도함수(PDF)는 다음과 같습니다.
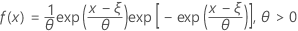
누적분포함수(CDF)는 다음과 같습니다.



표기법
| 용어 | 설명 |
|---|---|
| ξ | 위치 모수 |
| θ | 척도 모수 |
| e | 자연 로그의 밑 |
| v | Euler 상수(~0.57722) |
t-분포
- 분산을 알지 못하는 경우 정규 분포로부터 모평균의 신뢰 구간 생성
- 알지 못하지만 동일한 분산을 갖는 정규 모집단의 두 표본 평균이 유의하게 서로 다른지 여부 확인
- 회귀 계수의 유의성 검정
공식
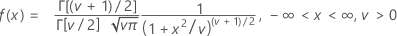
평균 = 0, ν > 0인 경우

표기법
| 용어 | 설명 |
|---|---|
| Γ | 감마 함수 |
| v | 자유도 |
| π | Pi (~3.142) |
삼각형 분포
삼각형 분포의 PDF는 삼각형 형상입니다.
공식
확률밀도함수(PDF)는 다음과 같습니다.
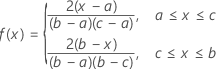

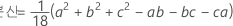
표기법
| 용어 | 설명 |
|---|---|
| a | 하한점 |
| b | 상한점 |
| c | 최빈값(PDF가 가장 높은 위치) |
균등 분포
균등 분포는 한 구간에 균일하게 분산된 데이터의 특성을 나타내며, a는 가장 작은 값이고 b는 가장 큰 값입니다.
공식
확률밀도함수(PDF)는 다음과 같습니다.


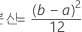
표기법
| 용어 | 설명 |
|---|---|
| a | 하한점 |
| b | 상한점 |
Weibull 분포
Weibull 분포는 제품 고장 시간을 모형화하는 데 유용합니다.
공식
확률밀도함수(PDF)는 다음과 같습니다.
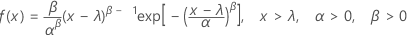
누적분포함수(CDF)는 다음과 같습니다.

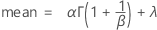
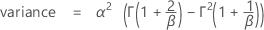
표기법
| 용어 | 설명 |
|---|---|
| α | 척도 모수 |
| β | 형상 모수, β = 1인 경우 Weibull PDF는 지수 PDF와 같습니다. |
| λ | 분계점 모수 |
| Γ | 감마 함수 |
| exp | 자연 로그의 밑 |
참고
일부 참고 문헌에서는 1/α를 모수로 사용합니다.
