1단계: 데이터가 분포를 따르는지 여부 확인
- p-값 ≤ α: 데이터가 분포를 따르지 않음(H0 기각)
- p-값이 유의 수준보다 작거나 같으면 귀무 가설을 기각하고 데이터가 분포를 따르지 않는다는 결론을 내립니다.
- p-값 > α: 데이터가 분포를 따르지 않는다는 결론을 내릴 수 없음(H0 기각 실패)
- p-값이 유의 수준보다 크면 데이터가 분포를 따르지 않는다는 결론을 내릴 충분한 증거가 없기 때문에 귀무 가설을 기각할 수 없다고 결정됩니다. 그러나 데이터가 분포를 따른다는 결론을 내릴 수 없습니다.
검정에 사용할 여러 분포와 모수를 지정하는 방법에 대한 내용은 적합 분포선에서 확인하십시오.
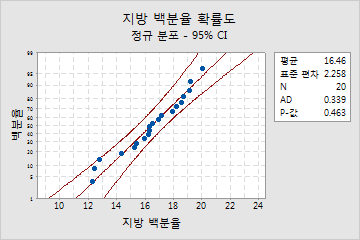
주요 결과: p-값
이 결과에서, 귀무 가설은 데이터가 정규 분포를 따른다는 것입니다. p-값이 0.463으로, 유의 수준 0.05보다 크기 때문에 귀무 가설을 기각할 수 없습니다. 데이터가 정규 분포를 따르지 않는다는 결론을 내릴 수 없습니다.
주의
표본 크기는 검정의 검정력에 영향을 미칩니다. 매우 작은 표본의 검정력은 유의한 분포 이탈도를 탐지하는 데 충분하지 않을 수 있습니다. 매우 큰 표본의 검정력은 너무 강해서 작고 중요하지 않은 분포 이탈도를 탐지하지 못할 수 있습니다. 따라서 2단계에 나와 있는 것처럼 확률도의 시각적 결과와 p-값을 함께 사용하여 분포 적합선을 평가하십시오.
2단계: 분포의 적합도 시각화
확률도를 조사하고 데이터 점들이 적합된 분포선을 얼마나 가깝게 따르는지 평가합니다. 이론적인 분포의 적합성이 양호하면 점들이 직선에 가까이 배열됩니다. 예를 들어 다음 정규 확률도의 점들은 적합된 선을 잘 따릅니다. 정규 분포는 데이터에 양호하게 적합한 것으로 보입니다.

참고
적합된 분포선은 그래프 중간의 직선입니다. 그림의 바깥쪽 실선은 분포 전체가 아닌 개별 백분위수의 신뢰 구간이며, 분포의 적합성을 평가하는 데 사용하지 않아야 합니다.
확률도 값의 시각적 평가에 대한 자세한 내용을 확인하려면 정규 확률도와 "두꺼운 연필 검정"으로 이동하십시오.
3단계: 각 모집단에 대해 추정한 백분위수 표시
Minitab에서 적합 분포선 위에 마우스 포인터를 올려놓으면 백분위수와 값 표가 표시됩니다. Minitab 데스크톱 앱에서 표를 보는 데 어려움이 있는 경우, 확률도를 두 번 클릭한 다음 편집 모드에서 적합 분포선 위에 마우스를 올려놓으세요.
예를 들어 다음 확률도는 런닝 머신에서 걷는 실험 대상자들의 맥박 수를 표시합니다. 정상 분포의 평균과 표준 편차가 데이터와 같은 경우, 모집단의 5%는 맥박 수가 55.46회 이하라고 기대됩니다.
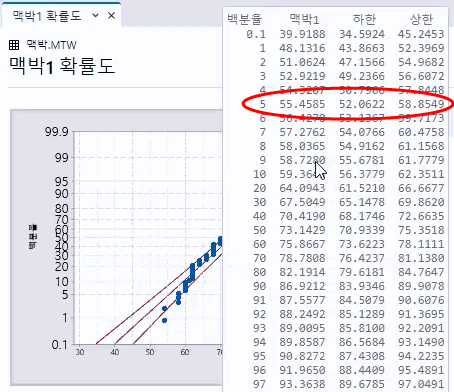
참고
추정된 모집단 백분위수는 데이터가 분포를 가깝게 따를 경우에만 정확합니다.
