평활기 선

평활기 선은 관계의 곡면성이 급격하게 변하지 않을 때 가장 유용합니다. 그래프에 추가되는 평활기 선은 Lowess 평활 방식을 사용하여 계산합니다.

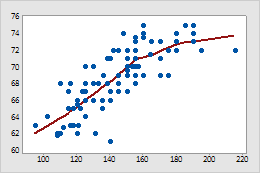
평활기 선이 있는 산점도

이 시계열도에서 평활기 선 하나는 실선이고 다른 평활기 선은 점선입니다.

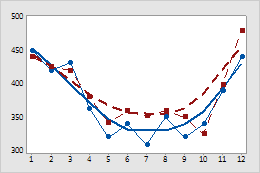
각 그룹별 평활기 선이 표시된 시계열도

Lowess 평활화 모수

평활도

0과 1 사이의 값을 입력할 수 있습니다. Lowness 평활기는 일반적으로 f 값이 변수 간의 내재되어 있는 관계를 왜곡시키지 않는 한도에서 평활된 적합을 나타내기에 충분히 클 경우 효과적입니다. Cleveland¹은 f를 가능한 크게 하고 y-값 잔차 대 x-값의 개별 Lowess 그림에서는 무관성을 유지하는 것이 좋다고 합니다.

단계 수

평활된 y-값에 대한 특이치의 영향력을 제한하려면 평활의 반복 횟수를 설정합니다. 0에서 10까지의 값을 입력할 수 있습니다. 각 단계에서는 이전 Lowess 단계에서 얻은 잔차의 크기를 기초로 하여 가중 선형 회귀의 다음 반복 과정에서 특이치에 주어지는 가중치를 줄입니다. Cleveland는 대부분의 데이터에 대한 특이치 효과를 올바르게 평활하는 두 가지 로버스트(Robust) 단계를 제안합니다

Lowess 평활 방식은 평활기 선을 결정하는 데 널리 사용되는 기술입니다. Lowess는 로컬 가중 산점도 평활기 선(locally-weighted scatterplot smoother)을 의미합니다. 평활화 정도와 특이치의 영향을 모두 수정하기 위해 모수를 지정할 수 있습니다.

Lowess 루틴에서는 각 x-값에 대한 평활된 새 y-값을 계산합니다.

1. 이 루틴은 (x,y) 점의 양쪽에 있는 x-값에서 가장 가까운 데이터를 사용하여 모든 점의 부분(기본값 f = 0.5)을 선택합니다. 이 부분을 평활의 정도라고 합니다. 이 방법을 선택하면 x-값을 기준으로 한 쪽의 점이 다른 쪽의 점보다 더 많이 선택될 수도 있습니다. 다음 예에서는 특정 점에 대해 선택된 데이터를 보여줍니다. 음영 영역에는 채워진 빨간색 데이터 점 가까이에 0.5가 있습니다.

   

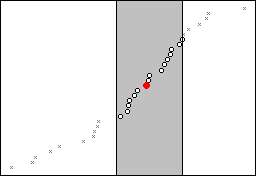
2. Minitab에서는 선택된 부분의 각 점과 평활할 점 사이의 x 거리를 사용하여 가중치를 계산합니다.

   

   다음 그래프는 선택된 점들의 부분에 대한 가중치(세로축)와 x-값(가로축) 사이의 관계를 보여줍니다. 각 x-값에 가장 가까운 점은 평활에서 가장 큰 가중치를 갖습니다.

   

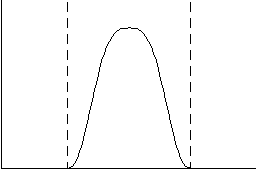
3. Minitab은 초기 평활된 값을 생성하는 2단계에서 계산된 가중치를 사용하여 선택된 부분에 있는 모든 점에 대해 가중 선형 회귀를 수행합니다.

4. 마지막으로 Minitab은 다음 방정식으로 얻은 새 가중치를 사용하여 반복한 3단계(기본 n = 2)를 통해 결과에 대한 특이치의 영향을 제한합니다.