지수 분포
계량형 포아송 공정의 사건 간 시간을 모형화하려면 지수 분포를 사용합니다. 여기서는 일정한 비율로 독립 사건이 발생한다고 가정합니다.
이 분포는 제품 및 시스템, 대기행렬 이론 및 Markov 체인의 신뢰도 분석과 같은 광범위한 용도에 사용됩니다.
- 전자 부품에 고장이 발생할 때까지 경과하는 시간
- 고객이 터미널에 도착하는 시간 간격
- 대기 중인 고객에게 서비스를 제공하는 시간
- 지불 불이행이 발생할 때까지 경과하는 시간(신용 위험 모형화)
- 방사성 원자핵이 붕괴될 때까지 경과하는 시간
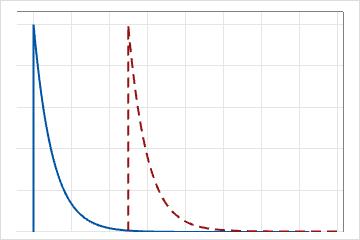
1-모수 지수 분포의 경우 분계점 모수가 0이며 이 분포는 척도 모수를 사용하여 정의됩니다. 1-모수 지수 분포의 경우 척도 모수가 평균과 같습니다.
무기억성의 의미
지수 분포의 중요한 특성은 기억되지 않는다(memoryless)는 것입니다. 사건의 확률은 과거 시행에 종속되지 않습니다. 따라서 발생률이 일정하게 유지됩니다.
기억되지 않는다는 특성은 부품의 남은 수명이 현재까지의 사용 기간과 무관함을 나타냅니다. 예를 들어, 동전 던지기의 랜덤 시행은 이러한 특성을 나타냅니다. 마모되거나 균열이 발생하여 나중에 고장날 가능성이 더 많은 시스템에는 기억되지 않는 특성이 없는 것입니다.
감마 분포
감마 분포는 오른쪽으로 치우쳐 있고 0보다 큰 양수 데이터 값을 모형화하는 데 사용합니다.감마 분포는 일반적으로 신뢰도 생존 연구에 사용됩니다. 예를 들어 감마 분포는 전기 부품이 고장나는 시기를 나타낼 수 있습니다. 한 가지 유형의 전자 부품은 대부분 같은 시간에 고장이 발생하지만, 몇 개의 부품은 오랜 시간이 지난 후에 고장날 수 있습니다.
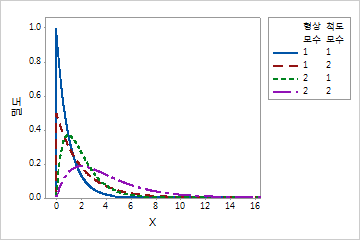
형상 모수가 정수인 경우 감마 분포를 Erlang 분포라고 부르기도 합니다. Erlang 분포는 대기행렬 이론 응용 분야에서 일반적으로 사용됩니다.
로지스틱 분포
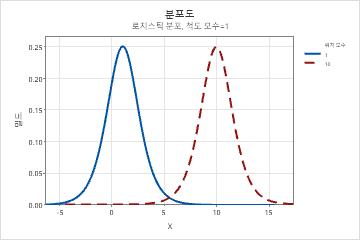
로지스틱 분포는 정규 분포보다 꼬리가 길고 첨도가 높은 데이터 분포를 모형화하는 데 사용합니다.
- 척도 모수의 영향
- 다음 그래프는 다양한 척도 모수 값이 로지스틱 분포에 미치는 영향을 보여줍니다.
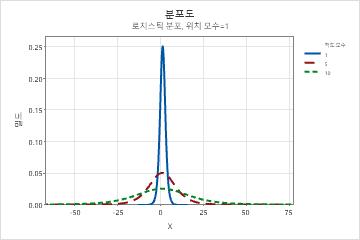
- 위치 모수의 영향
- 다음 그래프는 다양한 위치 모수 값이 로지스틱 분포에 미치는 영향을 보여줍니다.
로그 로지스틱 분포
변수 로그가 로지스틱 분포를 따르면 로그 로지스틱 분포를 사용합니다. 예를 들어, 로그 로지스틱 분포는 성장 모형의 생물 통계학 및 경제학과 같은 분야에서 이항 반응을 모형화하기 위해 사용됩니다.
로그 로지스틱 분포는 척도와 위치 모수를 사용하여 정의되는 계량형 분포입니다. 3-모수 로그 로지스틱 분포는 척도, 위치 및 분계점 모수를 사용하여 정의됩니다.
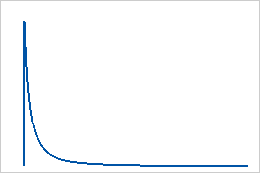
로그 로지스틱 분포는 Fisk 분포라고도 알려져 있습니다.
로그 정규 분포
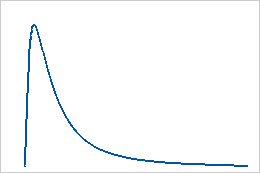
랜덤 변수의 로그가 정규 분포를 따르면 로그 정규 분포를 사용합니다. 로그 정규 분포는 랜덤 변수가 0보다 클 때 예를 들어, 신뢰도 분석 및 주식 변동의 모형화 등 재무 분야에 사용됩니다.
로그 정규 분포는 위치와 척도 모수에 의해 정의되는 계량형 분포입니다. 3-모수 로그 정규 분포는 위치, 척도 및 분계점 모수에 의해 정의됩니다.
정규 분포
정규 분포는 평균(μ)과 표준 편차(σ)에 의해 지정되는 계량형 분포입니다. 평균은 종 모양 곡선의 정점 또는 중심입니다. 표준 편차는 분포의 산포 정도를 나타냅니다.
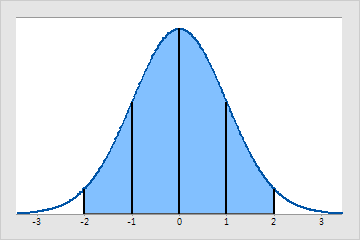
물리학, 생물학 및 사회적인 많은 측정 상황에서 자연스럽게 대략적인 정규성이 발생하기 때문에 정규 분포는 가장 일반적인 통계 분포입니다. 많은 통계 분석의 경우 데이터가 대략적으로 정규 분포를 따르는 모집단에서 추출된다고 가정합니다.
최소 및 최대 극단값 분포
최대 극단값 분포와 최소 극단값 분포는 밀접한 관계가 있습니다. 예를 들어 X가 최대 극단값 분포를 따르면 −X는 최소 극단값 분포를 따르며, 그 반대의 경우도 마찬가지입니다.
최소 극단값 분포
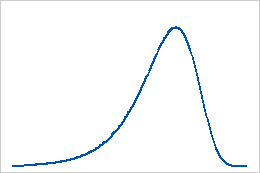
최대 극단값 분포
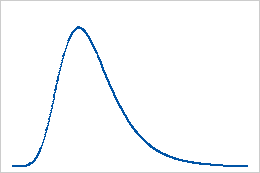
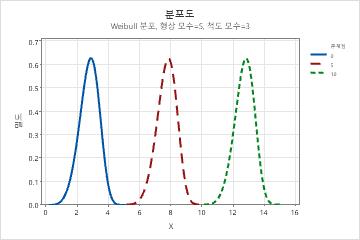
Weibull 분포
Weibull 분포는 공학, 의학 연구, 품질 관리, 재무 및 기상학 분야의 광범위한 응용 부문을 모형화할 수 있는 다용도 분포입니다. 예를 들어, 이 분포는 신뢰도 분석과 함께 수명 데이터를 모형화하기 위해 자주 사용됩니다. Weibull 분포는 공정 능력 분석에서 치우친 공정 데이터를 모형화하는 데도 사용됩니다.
Weibull 분포는 형상, 척도 및 분계점 모수를 사용하여 설명되며 3-모수 Weibull 분포로도 알려져 있습니다. 분계점 모수가 0인 경우 2-모수 Weibull 분포라고 합니다. 2-모수 Weibull 분포는 양수 변수에 대해서만 정의됩니다. 3-모수 Weibull 분포에는 0 및 음수 데이터도 사용할 수 있지만, 2-모수 Weibull 분포의 경우 모든 데이터가 0보다 커야 합니다.
모수들의 값에 따라 Weibull 분포는 여러 가지 형태를 가질 수 있습니다.
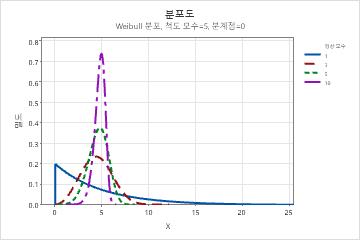
- 형상 모수의 효과
- 형상 모수는 데이터가 어떻게 분포되어 있는지 설명합니다. 형상이 3이면 정규 분포 곡선을 대략적으로 비슷하게 나타냅니다. 형상 값이 낮으면(1) 오른쪽으로 치우친 곡선을 나타냅니다. 형상 값이 높으면(10) 왼쪽으로 치우친 곡선을 나타냅니다.
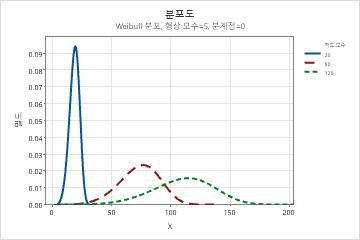
- 척도 모수의 효과
- 척도 또는 특성 수명은 데이터의 63.2 백분위수입니다. 척도는 Weibull 곡선의 분계점에 상대적인 위치를, 평균이 정규 곡선 위치를 이와 유사한 방식으로 정의합니다. 예를 들어, 척도 20은 장비의 63.2%가 분계 시간 후 첫 20시간 내에 고장난다는 것을 나타냅니다.
- 분계점 모수의 효과
- 분계점 모수는 0으로부터의 분포 이동을 설명하는데, 분계점이 음수이면 분포가 왼쪽으로 이동하며 분계점이 양수이면 분포가 오른쪽으로 이동합니다. 모든 데이터는 분계점보다 커야 합니다. 2-모수 Weibull 분포는 분계점이 0인 3-모수 Weibull 분포와 같은데, 예를 들어, 3-모수 Weibull(3,100, 50) 분포의 형상과 산포는 2-모수 Weibull 분포(3, 100)와 같지만 오른쪽으로 50 단위 이동합니다.