Y-척도 유형

히스토그램의 y-척도는 기본적으로 빈도를 나타내며(각 막대가 지정된 빈 내 값의 빈도를 나타냄) 각 빈의 크기를 강조합니다. 사용자가 공정 지식이 충분하지 않아 빈도 값을 이해할 수 없는 경우, 그래프의 y-척도 유형을 변경하여 빈도 값을 더 의미있는 형식인 백분율로 전환할 수 있습니다(각 막대가 해당 빈 내 모든 값의 백분율을 나타냄).

기본적으로 각 막대는 빈에 있는 값의 빈도를 나타냅니다. 각 막대가 빈에 있는 모든 값의 백분율을 나타내도록 하려면 y-척도 유형을 백분율으로 변경합니다. 분포를 비교하려고 하는데 표본 크기가 다를 경우에는 밀도을 사용합니다. 밀도은 막대를 비교할 때 빈의 너비가 같지 않은 경우에도 유용합니다. 밀도는 관측치 비율을 빈 너비로 나누어 계산됩니다.

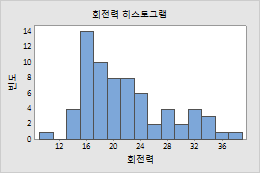
빈도(기본값)

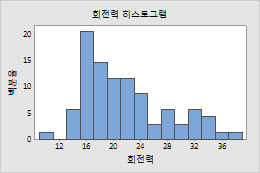
백분율

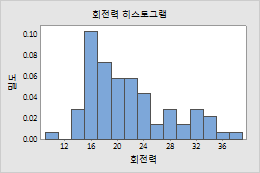
밀도

빈도

각 막대의 높이가 빈에 포함되는 관측치의 수를 나타냅니다.

백분율

각 막대의 높이가 빈에 포함되는 표본 관측치의 백분율을 나타냅니다. 백분율 척도가 있는 히스토그램은 경우에 따라 상대적 빈도 히스토그램이라고 합니다. 여러 크기의 표본을 비교하려면 백분율 척도를 사용하십시오.

밀도

각 막대의 면적은 빈에 포함되는 표본 관측치의 비율을 나타냅니다(비율 = 막대 면적 = 빈 너비 × 막대 높이).

누적 히스토그램: (빈도와 백분율 척도에만 해당) 막대 높이가 왼쪽에서 오른쪽으로 누적됩니다. 각 막대의 높이는 빈의 높이에 모든 이전 빈의 높이를 더한 값입니다.

백분율

y-축의 값이 추정된 누적 백분율을 나타냅니다. 추정된 누적 백분율은 추정된 누적 확률에 100을 곱한 값과 같습니다.

확률

y-축의 값이 추정된 누적 확률을 나타냅니다. x 값에 대한 누적 확률은 모집단에서 가져온 랜덤 관측치가 x보다 작거나 같을 확률입니다.

Minitab에서는 중위수 순위 방법(Benard 방법이라고도 함)을 사용하여 각 관측치에 대한 누적 확률(r)을 추정합니다.

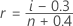
이 공식에서 i는 표본 내 관측치의 순위이며 n은 표본의 총 관측치입니다. 표본에서 가장 작은 값의 경우에는 i = 1이고 표본에서 가장 큰 값의 경우에는 i = n입니다.

점수(확률도에만 해당)

y-축의 값이 역 누적 확률을 나타냅니다.

정규 분포와 로그 정규 분포에 대한 점수 값은 표준 정규 분포를 사용하여 계산된 r의 역 누적 확률입니다.

지수 분포와 Weibull 분포의 점수 값은 LN(−LN(1−r))로 계산되며, 여기서 LN은 자연 로그 함수입니다.

유사성(기본값)

각 군집의 높이가 유사성을 나타냅니다. 두 군집 i와 j 사이의 유사성 s(ij)는 100 (1 - d(ij) / d(max))로 계산됩니다. 분석을 위해 원래 거리 행렬 D를 입력하는 경우 d(max)는 D의 최대값입니다. D가 데이터에서 계산되면 상관 계수를 거리 측도로 선택한 경우 d(max) = 2이고 절대 상관 계수를 거리 측도로 선택한 경우 1입니다.

거리

각 군집의 높이가 거리를 나타냅니다.