マクロをダウンロードする
ダウンロードしたマクロの場所をMinitabが見つけられるようにします。を選択します。マクロの位置で、マクロファイルを保存する場所を参照します。
重要
古いWebブラウザを使用している場合、[ダウンロード]ボタンをクリックしたときに、Minitabマクロと同じ.mac拡張子を使用するQuicktimeでファイルが開く場合があります。マクロを保存するには、[ダウンロード]ボタンを右クリックして[対象をファイルに保存]を選択します。
必須入力項目
最大5つまでの計画行列
オプション入力
- MODEL モデルタイプ
- 実験の実行時に検定されるモデルを指定します。デフォルトは"interaction"です。linear、quadratic、interaction、purequadraticなどの複数のモデルを入力できます。各モデルには次の項が含まれます。
- Linear: 定数および線形項
- Interaction: 定数、線形、および積和項
- Quadratic: 交互作用および2次項
- Purequadratic: 定数、線形、および2次項
- RESOLUTION K
- 半径の各個別値で最小、最大、および積分予測分散を推定するために使用される、サンプル計画点の数を指定する場合に使用します。回転可能な計画の場合、小さい分解能を選択できます。回転が不可能な計画の場合、因子数の増加に伴い分解能の増加が必要な可能性があります。デフォルトは500計画点です。
- INCREMENT K
- 半径の増分を指定する場合に使用します。この値を変更することで、分解能の大きさが異なるグラフを表示できます。デフォルト値は0.1コード化単位です。
- MAXDIST K
- 最大半径距離を指定します。デフォルトでは、計画の中心から最も離れた計画点に対する最大距離が定義されます。複数の計画に基づくVDGの場合、MAXDISTはすべての計画からの最大距離に設定されます。
マクロの実行
CCDの因子が行列M1にコピーされていて、Box-Behnken計画の因子がM2に保存されているとします。マクロを実行するには、を選択し、次のコマンドを入力します。
%VDG M1 M2;
MODEL "quadratic";
RESOLUTION 150.実行をクリックします。
詳細情報
分散の散布度グラフと実験計画
分散の散布度グラフは、実験計画(DOE)を選択する工程で使用されるグラフツールです。このグラフには、計画空間全体のDOEのスケール化された予測分散が表示され、通常は応答曲面計画の比較に使用されます。ただし、線形モデル、交互作用項のある線形モデル、2次項のある線形モデル、または完全2次モデルなど、特定のモデルで複数の計画の性能を比較するために分散の散布度グラフを使用することもできます。
VDGの歴史と背景
VDGはそもそも、Giovannitti-JensenおよびMyers(1989)、Myersら (1992)によって、計画空間全体のスケール化された予測分散の安定性のスナップショットを表示するために開発されました。
数学的に、スケール化された予測分散は次の式で推定できます。
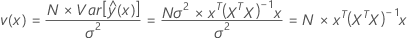
ここで、v(x)は点xでのスケール化された予測分散で、上記のように、応答データには依存せずに計画行列Xのみに依存します。つまり、スケール化された予測分散は、実験の実行数、共分散行列、および予測分散を評価している点の関数です。VDGで表示されるスケール化された予測分散は応答データとは独立しているため、VDGで事前に計画の利点を評価できます。
一般に、VDGは次の4つの基本成分で構成されます。
- · 半径rに対する球面分散のプロット。球面分散では、半径rの球面上でv(x)が平均(積分)されます。
- · 原点から開始するrの複数の値における半径r上の最大予測分散のプロット(rは0から開始し、原点から最も離れた計画点に達するまで小さく増分していきます)。
- · 原点から開始するrの複数の値における半径r上の最小予測分散のプロット。
- · v(x) = pでの水平線。ここで、pは適合されるモデルのパラメータ数です。「 最適」計画は、計画空間のすべての点において最大予測分散がp以下となります。
VDGには、指定された点から原点または計画の中心までの距離を表すrの異なる値における、スケール化された平均、最大、および最小予測分散が表示されます。
計画のその他の面を評価するためのVDGの使用
VDGを使用すると、1つの計画の性能をその予測分散に基づいて評価できます。複数の計画の比較にVDGを使用することもできます。VDGの別の応用として、計画に中心点を追加したことによる効果の評価があります。
さらに、計画が回転可能であるかどうかも評価できます。回転可能な計画では、グラフ内の3つすべてのライン(最小、平均、および最大)が一致します。最小、平均、および最大ラインが一致しない場合、面心計画は回転できません。
予測分散を推定するモンテカルロシミュレーション
この詳細セクションでは、VDGに表示される最小、最大、および平均予測分散に使用される数学的方法について説明します。VDGを表示して解釈するマクロの実行方法に関する情報のみが必要な場合、このセクションはスキップしてください。
前述のとおり、半径の固定値の場合、スケール化された最小、最大、および積分予測分散を調べるには、検索を実行する必要があります。Minitabマクロで選択されている方法は、モンテカルロシミュレーション、および計画の中心x = (0,0,…,0)Tから等距離にある点で一様に検索する機能に基づいています。
原点からの異なる距離で、1)最小予測分散、2)最大予測分散、3)積分予測分散の3つの数量を計算する必要があります。これらの数量を調べるには、いくつかの方法があります。1つの方法は、非線形プログラミングアルゴリズムを使用して最小および最大予測分散を調べることです。ただし、Minitabでこれらの数量の推定に使用する方法は、異なるr値で一様にサンプル抽出し、計画の中心から同じ距離にある個別の点を見つけます。等距離にある点の空間から、2つの条件を満たすことで最小および最大予測分散が適切に推定されます。この1つ目の条件は、等距離にある点のサンプル抽出は一様な必要があるということです。つまり、一部の等距離にある点が他の点よりも選択される確率が高くなる領域があってはなりません。2つ目の条件は、考えられる計画点の空間全体を覆うのに十分な大きさの点の数が必要であるということです。
サンプル抽出が必要なすべての点は等距離であるため、サンプル抽出の問題は、指定された半径のn球または超球から点を取得する適切な方法を見つけることです。
この手順はMarsaglia(1972)によって説明されており、その要約を次に示します。
- 正規確率変数n次元ベクトルを作成します(たとえば、標準正規分布から)。このベクトルをx = (x1, x2,…,xn)とします。複数のベクトルxを作成します。
- 作成したすべてのx点の半径ρを計算します。

- ベクトルxの各エントリにrを掛けて、ステップ1で取得した元の計画点をそれぞれ変換します。ここでは、rは、サンプルの抽出元の超球の半径を表しています。
一定半径rの超球の点をサンプル抽出する方法を説明しました。このサンプル抽出方法を使用して、最大または最小予測分散を推定できます。大数の弱法則によって、これらのサンプル抽出された計画点の平均予測分散を使用して、nが大きい限り真の積分予測分散を推定できます。
参考文献
[1] Marsaglia G. "Choosing a Point from the Surface of a Sphere". The Annals of Mathematical Statistics, Vol. 43, No. 2 (1972), pp. 645-646.
[2] Myers R, Montgomery D. (2002). Response Surface Methodology - Process and Product Optimization Using Designed Experiments, Second Edition. John Wiley & Sons, Inc.
