マクロをダウンロードする
ダウンロードしたマクロの場所をMinitabが見つけられるようにします。を選択します。マクロの位置で、マクロファイルを保存する場所を参照します。
重要
古いWebブラウザを使用している場合、[ダウンロード]ボタンをクリックしたときに、Minitabマクロと同じ.mac拡張子を使用するQuicktimeでファイルが開く場合があります。マクロを保存するには、[ダウンロード]ボタンを右クリックして[対象をファイルに保存]を選択します。
必須入力項目
- 応答データの列
- 因子の非コード化水準を含む対応する列
オプション入力
- STORE C-C
- 最も急な上昇/下降経路をワークシートに保存します。この入力では、経路が保存されるワークシートの列を指定します。因子ごとに1つの保存列を指定します。このサブコマンドが指定されていない場合、経路は表示されますが、ワークシートには保存されません。
- STEP K
- プロセス変数（
）のステップサイズまたは増分をコード化単位で定義します。デフォルトでは、増分は1です。 - BASE C
- 最も急な上昇/下降経路のステップサイズを定義します。入力bは、ステップサイズを定義する係数の列です。デフォルトでは、ステップサイズは絶対値が最大の因子係数です。
- DESCENT
- 最も急な上昇経路（デフォルト）の代わりに最も急な下降経路の計算を指定します。
- RUNS K
- 生成する連の数を指定します。入力rは定数です。デフォルトでは、連の数は5です。
マクロの実行
2因子計画があり、因子がc5とC6、応答がC7に保存されているとします。この場合に応答を最大化できる可能性がある経路を調べます。さらに、この経路をワークシートの列C9～C10に保存します。連の間のステップサイズは2（コード化単位）である必要があり、C5に含まれる因子が基本因子になります。最後に、最も急な上昇経路に沿った8つの連を計算します。最後に、最も急な上昇経路に沿った8つの連を計算します。
%ASCENT C7 C5-C6;
STORE C9-C10;
STEP 2;
BASE C5;
RUNS 8.実行をクリックします。
詳細情報
応答曲面法の概要
応答曲面法（RSM）では、制御可能な因子の最適な設定を判断することで対象となる応答を最適化できます。したがって、RSMの基本的な目標は、最適な設定
.
これを行うために逐次実験を使用できます。通常は、因子または一部実施要因計画から開始して無関係な因子をスクリーニングします。応答の回帰モデルを取得したら、最も急な上昇経路に沿って外挿および実験します。最後に、応答曲面計画を選択して曲面性をモデル化し、最適な応答を見つけます。
RSMの3つの基本ステップは以下のとおりです。
- 因子スクリーニング実験を行う。
- 最も急な上昇経路または下降経路に従う。
- 2次回帰モデルを適合して最適化する。
次のセクションでは、2つの例を使用して最も急な上昇経路がどのように計算されるかについて説明し、このタスクを実行するMinitabマクロを提供します。
最も急な上昇/下降経路とは
スクリーニング実行を行って（主効果のみの）応答の線形モデルを取得したら、応答をすばやく改善する方向に移動できます。応答を最大化するには、最も急な上昇経路に従います。応答を最小化するには、最も急な下降経路に従います。
最も急な上昇/下降経路の計算
最も急な上昇経路を計算するには、最初にモデルを適合する必要があります。実験に2つの因子があり、因子x1とx2の間の交互作用は有意ではないとします。この実験のモデル式は次のとおりです。
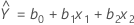
ここで、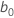
は切片の推定で、
, 
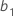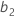はそれぞれ因子
および
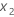の係数です。
モデル式の取得後は、次の手順を実行します。
- 「基本因子」として1つのプロセス変数を選択し、基本因子のステップサイズまたは増分(
) iを識別します。
注
デフォルトでは、基本因子が指定されていない場合は、絶対回帰係数
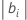が最大の変数がマクロによって選択されます。 - 次の式を使用して、他のプロセス変数の増分を判断します。
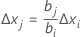
- 増分をコード化単位から非コード化単位に変換します。
Quality Companionでの最も急な上昇の形式
Quality Companion 2の標準形式を使用して、最も急な上昇/下降経路を計算することもできます。基本因子、因子の非コード化水準、増分を指定することで入力パラメータを入力して、必要な数の連を追加するだけです。
例1: エッチング速度の最大化
次の例は、マイヤーズとモンゴメリーによる『Response Surface Methodology: Process and Product Optimization Using Designed Experiments』に記載されている内容をカスタマイズしたものです。
半導体製造の目標は、因子の極間距離（ギャップ）と陰極への電力（電力）の水準を変化させることでプラズマエッチング速度を最大化することです。実験を行うことで次のモデルが得られるとします。
ここで、
はギャップを表し、
は電力を表します。
マクロを使用して最も急な上昇経路を計算するには、最初に非コード化単位の応答と主効果（
および
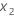）に対応するワークシートの列を識別します。この例では、応答（エッチング速度）はC7にあり、主効果（ギャップと電力）はC5とC6にあります。
マクロを実行するには、に移動し、次のコマンドを入力します。
%ASCENT C7 C5-C6;
STORE C9-C10.注
使用しているマクロのバージョンがASCENT17.macである場合は、「%ASCENT」ではなく、「%ASCENT17」と入力します。
コマンドを発行するをクリックします。
ワークシートのデータを使用することで、Minitabは最も急な上昇経路に5つの連を作成し、経路を列C9とC10に保存します。最終モデルに2つの因子のみが含まれる場合、最も急な上昇/下降経路を表示する散布図を作成できます。
例2: 反応収量の最小化
この例は、マイヤーズとモンゴメリーによって作成されたものを、最も急な上昇経路の代わりに最も急な下降経路を使用するようにカスタマイズしています。
実験の目標は、制御可能な4つの因子、A（反応物質Aの量）、B（反応時間）、C（反応物質Cの量）、およびD（温度）の最適な設定を特定して反応収量を最小化することだとします。4つの因子の非コード化（自然）水準は、因子Aは10および15グラム、因子Bは1および2分、因子Cは25および35グラム、因子Dは75および85 °Cです。さらに、基本係数は反応物質Aに対応し、ステップサイズは非コード単位の1グラムです。適合されたモデルは次のとおりです。
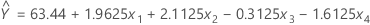
マクロを使用して最も急な下降経路を計算するには、サブコマンドDESCENTを使用します。反応物質Aに対応する列はC5であるため、BASEの入力はC5です。因子Aのコード化単位は2.5グラムに等しいため、コード化単位のSTEPは1/2.5 = 0.4です。マクロを実行するには、に移動し、次のコマンドを入力します。
%ASCENT C9 C5-C8;
STORE C11-C14;
STEP 0.4;
BASE C5;
DESCENT;
RUNS 10.注
使用しているマクロのバージョンがASCENT17.macである場合は、「%ASCENT」ではなく、「%ASCENT17」と入力します。
注
元の文献にある例の出力を得るには、最も急な上昇経路を使用して改善方向を計算します。次に示すように、DESCENTサブコマンドなしでコマンドのブロックを発行します。
%ASCENT C9 C5-C8;
STORE C11-C14;
STEP 0.4;
BASE C5;
RUNS 10.参考文献
R. Myers and D. Montgomery (2002). Response Surface Methodology - Process and Product Optimization Using Designed Experiments, Second Edition. John Wiley & Sons, Inc.
