マクロをダウンロードする
ダウンロードしたマクロの場所をMinitabが見つけられるようにします。を選択します。マクロの位置で、マクロファイルを保存する場所を参照します。
重要
古いWebブラウザを使用している場合、[ダウンロード]ボタンをクリックしたときに、Minitabマクロと同じ.mac拡張子を使用するQuicktimeでファイルが開く場合があります。マクロを保存するには、[ダウンロード]ボタンを右クリックして[対象をファイルに保存]を選択します。
必須入力項目
- 数値応答データの列
- 対応する因子水準の列
注
サブコマンドUNSTACKEDを指定することで、積み重ねを解除したデータを使用できます。
オプション入力
- UNSTACKED
- データの積み重ねを解除する場合に指定します。
- FALPHA
- 目的の全体α水準(デフォルトは0.20)を指定する場合に使用します。
- CONTROL C
- 対照となる列(C)を指定する場合に使用します。
注
データが積み重ねられている場合、対照群の応答とその他の因子水準の応答を同じ列にすることはできません。対照群の応答は個別の列にする必要があります。
マクロの実行
応答データがC1にあり、因子水準がC2にあるとします。マクロを実行するには、を選択し、次のコマンドを入力します。
%KRUSMC C1 C2実行をクリックします。
出力
出力の最初の部分には、実行される比較数(k)、
 、全体α(α)、Bonferroniの個別α(β)、
、全体α(α)、Bonferroniの個別α(β)、 、および両側の棄却z値が表示されます。
、および両側の棄却z値が表示されます。
次のセクションには、Minitabの標準化された群平均の順位差(θ)およびこの差に関連付けられたp値が表示されます。これらの表は対称的であるため、表の上の三角部にアスタリスクが表示されます。また、対角は群とそれ自体の比較(この比較は無意味で分析では考慮されない)を表すため、表の対角の下に0が表示されます。この表の見方の例として「群2と群4間の差は何か?」があります。3番目のセクションには、中央値の符号信頼区間が表示されます。これらの区間の信頼水準は、全体αで制御されます。これらの区間はすべての全体αで制御されるため、ペアワイズで比較できます(付録2)。すべてまたは一部の区間で目的の信頼は達成できない場合があることに注意してください。また、全体αによるこの「全体」の範囲はサンプルサイズが異なる場合は正確ではありませんが、通常は妥当な近似となります。
最後のセクションには、「有意な」差(存在する場合)が表示されます。このセクションでは、z値、棄却z値、およびz値に関連付けられたp値が示されます。
グラフには、非絶対群平均順位の標準化された差が表示されます。このグラフは群の差の大きさだけでなく方向も確認できるため、非常に役立ちます。また、正と負の棄却z値も表示され、差が「有意」であるかどうかを確認できます。
同順位のデータ
同順位のデータがある場合、不偏化のための定数(または修正因子)2が計算されます。H統計量は調整済み3です。標準偏差(ξ)は、この修正因子4でも調整されます。出力には、調整された表と未調整の表の両方が設定されます。ただし、Minitabでは調整済みの表を使用する必要があるため、調整済みの表のp値のみを提供します。未調整の表を表示する主な理由は、z値に同順位がどのように影響するかを示すためです。同順位が非常に多い場合、検定は分布が連続分布であると仮定するため、データの妥当性は正確ではありません。通常、同順位は結論にほとんど影響しません。
謝辞
このマクロのレビュー、この作業に関する多くの議論、およびこれまでに費やされた時間と忍耐に対して、Dr. Tom Hettmansperger氏(ペンシルベニア州立大学)に感謝の意を表します。また、マクロ関連の提案と批評に対して、Nicholas Bolgiano氏とMike Delozier氏(Minitab, Inc.)に感謝の意を表します。
追加情報
Dunnの検定
ペアワイズの同時推定を行う効果的な方法がDunn(1964)によって導入されました。最初にデータを組み合わせてから順位を付け、群の平均順位を求めてそれらの平均順位の標準化された絶対差を取得します。
kは処理の数で、
次のように定義します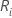 はi番目の処理の順位の合計で、i = 1,…,kとします。
はi番目の処理の順位の合計で、i = 1,…,kとします。
次のように定義します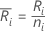
ここで、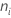 はi番目の処理における観測値の数です。
はi番目の処理における観測値の数です。
次のように定義します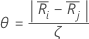
ここで、j=l,...,k、j  i
i
ここで、
H統計量
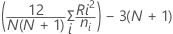
ここで、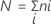
次の場合に「有意性」があるとします。

ここで、
αは指定された全体α値、
