フィッシャーの正確検定
フィッシャーの正確検定は独立性の検定です。検定は、ピアソンの検定と尤度比の検定で用いられるおおよそのカイ二乗分布よりも、正確検定に基づいています。フィッシャーの正確検定は、期待セル度数が小さく、カイ二乗の近似値があまり良くない時に、役に立ちます。
計算式
- 母集団サイズ
- 合計観測数
- 母集団の成功数
- 最初の行の観測数
- サンプルサイズ
- 最初の列の観測数
例
| こども | 大人 | 行の合計 | |
|---|---|---|---|
| 砂糖 | 9 | 1 | 10 |
| チョコチップ | 2 | 8 | 10 |
| 列の合計 | 11 | 9 | 20 |
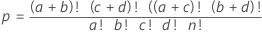
| こども | 大人 | 行の合計 | |
|---|---|---|---|
| 砂糖 | a | b | a+b |
| チョコチップ | c | d | c+d |
| 列の合計 | a+c | b+d | a+b+c+d |
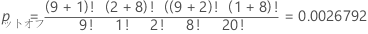
この例では、他の可能な行列のpカットオフ以下のp値の合計は0.0054775です。
マクネマーの正確検定
マクネマーの検定は、処理前と処理後に観測された比率を比較します。たとえばマクネマーの検定を使用して、トレーニングプログラムによって質問に正しく解答する参加者の比率が変化するかどうかを判断できます。
マクネマーの検定の観測値は、次に示される2 x 2表に要約することができます。
| 処理後 | |||
| 処理前 | 真の状態 | 偽の状態 | 合計 |
| 真の状態 | n11 | n12 | n1. |
| 偽の状態 | n21 | n22 | n2. |
| 合計 | n·1 | n·2 | n·· |
トレーニングの例の状態は正しい答えです。したがって、n21は、トレーニング前とは違い、トレーニング後に質問に正しく答える参加者の数です。そしてn12は、トレーニング後とは違い、トレーニング前に質問に正しく答える参加者の数です。参加者の総数がn..で示されています。
推定差
母集団におけるp1.- p.1の周辺確率の間の差をδとします。推定差、 、は次の計算式で得られます。
、は次の計算式で得られます。
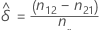
信頼区間
おおよそ100(1 – α)%の信頼区間は、次の計算式で得られます。

ここではαが検定の有意水準、z α/2がα/2のしっぽ確率と関連性のあるz得点で、標準誤差(SE)は次の計算式で得られます。
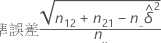
p値
帰無仮説はδ = 0。帰無仮説の検定の正確なp値は次のように計算されます。

ここではXが、0.5の事象確率とn21 + n12に等しい試行回数の二項分布から描画されるランダム変数です。
コクラン-マンテル-ヘンツェル検定
この検定では三元交互作用が存在しないと仮定しています。検定の目的は、確率変数を管理しながら、2つの二値変数の間の関係度を評価することです。CMH統計量は、自由度が1のカイ二乗の百分位と比較されます。
コクラン-マンテル-ヘンツェル(CMH)検定は、3ないしはそれ以上の分類変数が存在し、最初の2つの変数のそれぞれに2つの水準がある場合に、適用されます。最初の2つの変数を超えたすべての変数は、CMH検定の目的では単一変数Zとして扱われ、水準のそれぞれの組み合わせは水準Zとして扱われます。
計算式
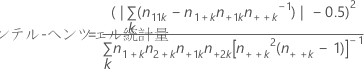
表記
| 用語 | 説明 |
|---|---|
| k | 水準Z |
| n11k | 最初の行、最初の列の観測数 |
| n1+k | 最初の行、最初の列の観測数 |
| n+1k | 最初の列の観測数 |
| n++k | 合計観測数 |
| n2+k | 2番目の行の観測数 |
| n+2k | 2番目の列の観測数 |
