好きな方法または計算式を選択します。
クレイマーのV2
クレイマーのV2は、ピアソンのカイ二乗統計量に基づいて、関連性が計られます。
計算式

表記
| 用語 | 説明 |
|---|---|
| χ2 | ピアソンカイ二乗統計量 |
| r | 行数 |
| c | 列数 |
| n++ | 合計観測数 |
κ統計量
κによって、カテゴリのセットに単位を割り当てる2人の判定者の間の一致レベルが計られます。κ値1は完全な一致に相当します。κ値0は偶然の所産として期待されるほどの一致ではないことを反映しています。
計算式

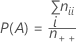
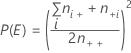
表記
| 用語 | 説明 |
|---|---|
| ni+ | i行目の観測数 |
| n+i | i列目の観測数 |
| nii | i行目でi列目のセルの観測数 |
| n++ | 合計観測数 |
λ
グッドマン-クラスカルのλは、名義水準変数のクロス集計における関連の度合いを表します。変数(行変数または列変数)の値が与えられた場合に、その変数の独立変数(列変数または行変数)の予測可能性の向上をλは計ります。誤判別の確率は、最大確率のカテゴリに対する割り当てに基づいて計算されます。
計算式
独立変数としてのY(列変数)を使用して、λは次のように計算されます。
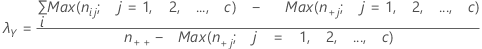
独立変数としてのX(行変数)を使用して、λは次のように計算されます。

表記
| 用語 | 説明 |
|---|---|
| c | 列数 |
| r | 行数 |
| ni+ | i行目の観測数 |
| n+j | j列目の観測数 |
| nij | i行目でj列目のセルの観測数 |
| n++ | 合計観測数 |
τ (タウ)
グッドマン-クラスカルのτは、名義水準変数のクロス集計における関連の度合いを表します。変数(行変数または列変数)の値が与えられた場合に、その変数の独立変数(列変数または行変数)の予測可能性の向上をτは計ります。誤判別の確率は、周辺比率または条件付き比率によって指定される確率のランダムカテゴリ指定に基づきます。
計算式
独立変数としてのY(列変数)を使用して、τは次のように計算されます。
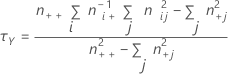
独立変数としてのX(行変数)を使用して、τは次のように計算されます。
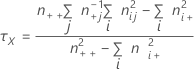
表記
| 用語 | 説明 |
|---|---|
| ni+ | i行目の観測数 |
| n+i | j列目の観測数 |
| nij | i行目でj列目のセルの観測数 |
| n++ | 合計観測数 |
