目的の方法または計算式を選択してください。
各カテゴリの期待値
計算式
各カテゴリiの期待値Eは次のように計算されます。
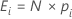
表記
| 用語 | 説明 |
|---|---|
| pi | i番目のカテゴリの検定比率で、1/kまたは入力する値に等しい |
| k | 知覚区分数 |
| N | 総観測値(O1 + ... + Ok) |
| Oi | i番目のカテゴリの観測値 |
カイ二乗検定統計量
計算式
カイ二乗検定統計量は、次のように計算します。
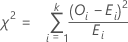
表記
| 用語 | 説明 |
|---|---|
| k | 知覚区分数 |
| Oi | i番目のカテゴリの観測値 |
| Ei | i番目のカテゴリの期待値 |
カイ二乗統計量への寄与
計算式
i番目のカテゴリのカイ二乗への寄与度は次の通りです。

表記
| 用語 | 説明 |
|---|---|
| Oi | i番目のカテゴリの観測値 |
| Ei | i番目のカテゴリの期待値 |
自由度(DF)
計算式
自由度(DF)は次のように計算されます。

表記
| 用語 | 説明 |
|---|---|
| 自由度(DF) | 自由度 |
| k | カテゴリの数 |
p値
計算式
p値は次のように計算されます: 確率 (Χ > 検定統計量)
表記
| 用語 | 説明 |
|---|---|
| X | は自由度k – 1のカイ二乗分布に従う |
計算例
次の通り仮定:
| カテゴリi | 観測されたOi | 検定比率pi |
|---|---|---|
| A | 5 | 0.1 |
| B | 15 | 0.2 |
| C | 10 | 0.3 |
| D | 10 | 0.4 |
| N=40 |
算出:
| カテゴリi | 期待値
Ei = (pi * N) |
カイ二乗への寄与度
(Oi- Ei)2 / Ei |
|---|---|---|
| A | 0.1 * 40 = 4 | (5 – 4)2 / 4 = 0.25 |
| B | 0.2 * 40 = 8 | (15 – 8)2 / 8 = 6.125 |
| C | 0.3 * 40 = 12 | (10 – 12)2 / 12 = 0.3333 |
| D | 0.4 * 40 = 16 | (10 – 16)2 / 16 = 2.25 |
χ2 = 0.2500 + 6.1250 + 2.2500 + 0.3333 = 8.9583
自由度(DF) = k – 1 = 3
p値 = 確率 (Χ > 8.9583) = 0.0299
表記
| 用語 | 説明 |
|---|---|
| 自由度(DF) | 自由度 |
| k | カテゴリの数 |
