カイ二乗値への寄与度の図
この棒グラフは各カテゴリのカイ二乗統計量全体への寄与度をプロットします。最大の寄与から最小の寄与まで、寄与別にカテゴリを並べる図を選択します。
解釈
観測値と期待値に大きな差のあるカテゴリは、カイ二乗統計量全体への寄与度を大きくします。
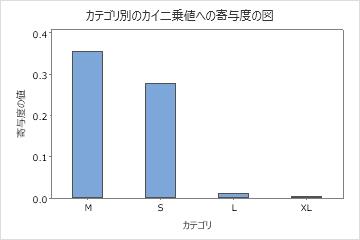
この棒グラフは、カイ二乗統計量への最大の寄与度が中カテゴリにあることを示します。
観測値と期待値の図
各カテゴリの観測値および期待値を示す棒グラフを用いて、特定のカテゴリで差があるかを判別します。
観測度数と期待度数の間の差が統計的に有意であると判断した場合、どのカテゴリで観測値と期待値の差が最大かを判定するのに、この棒グラフを用いることができます。

この棒グラフは、観測値が各カテゴリの期待値に非常に似ていることを示しています。したがって、棒グラフはp値が示していることを視覚的に確認し、観測比率が特定の比率と有意に異なると結論付けることはできません。
カイ二乗とカイ二乗への寄与度
個別のカテゴリ寄与度を用いて、総カイ二乗統計量がどの程度、各カテゴリの観測値と期待値の差に起因しているのかを計ります。
Minitabでは、各カテゴリのカイ二乗統計量への寄与度が、そのカテゴリの期待値で割った、カテゴリの観測値と期待値の差の平方として計算されます。カイ二乗統計量はすべてのカテゴリのこれらの値の和です。
解釈
観測値と期待値に大きな差のあるカテゴリは、カイ二乗統計量全体への寄与度を大きくします。
観測度数と期待度数
| カテゴリ | 観測値 | 検定比率 | 期待 | カイ二乗への寄与度 |
|---|---|---|---|---|
| S | 25 | 0.1 | 22.5 | 0.277778 |
| M | 41 | 0.2 | 45.0 | 0.355556 |
| L | 91 | 0.4 | 90.0 | 0.011111 |
| XL | 68 | 0.3 | 67.5 | 0.003704 |
カイ二乗検定
| N | 自由度 | カイ二乗 | p値 |
|---|---|---|---|
| 225 | 3 | 0.648148 | 0.885 |

自由度(DF)
カイ二乗適合度検定の自由度は、カテゴリ数–1になります。
解釈
Minitabでは、自由度を使用してp値を判断します。研究のカテゴリが多いほど、自由度が高くなります。
これらの結果では、自由度(DF)は3です。
カイ二乗検定
| N | 自由度 | カイ二乗 | p値 |
|---|---|---|---|
| 225 | 3 | 0.648148 | 0.885 |
N
Nは総サンプルサイズです。Nは観測度数全ての和に等しいです。
解釈
これらの結果では、総サンプルサイズ(N)は225です。
観測度数と期待度数
| カテゴリ | 観測値 | 検定比率 | 期待 | カイ二乗への寄与度 |
|---|---|---|---|---|
| S | 25 | 0.1 | 22.5 | 0.277778 |
| M | 41 | 0.2 | 45.0 | 0.355556 |
| L | 91 | 0.4 | 90.0 | 0.011111 |
| XL | 68 | 0.3 | 67.5 | 0.003704 |
カイ二乗検定
| N | 自由度 | カイ二乗 | p値 |
|---|---|---|---|
| 225 | 3 | 0.648148 | 0.885 |
観測値と期待値
観測値は、カテゴリに属するサンプル内の観測実数です。
期待値は検定比率が真の場合に、平均的に、発生しそうな観測値の数です。Minitabでは、各カテゴリの検定比率に総サンプルサイズを掛けて、期待度数を計算します。
解釈
出力表または棒グラフを用いて、観測値と期待値を比べることができます。
観測度数と期待度数
| カテゴリ | 観測値 | 検定比率 | 期待 | カイ二乗への寄与度 |
|---|---|---|---|---|
| S | 25 | 0.1 | 22.5 | 0.277778 |
| M | 41 | 0.2 | 45.0 | 0.355556 |
| L | 91 | 0.4 | 90.0 | 0.011111 |
| XL | 68 | 0.3 | 67.5 | 0.003704 |

p値
p値は帰無仮説を棄却するための証拠を測定する確率です。確率が低いほど、帰無仮説を棄却する強力な証拠となります。
p値を用いて、帰無仮説を却下するか却下できないかを判断し、各カテゴリの母比率が各カテゴリの特定の値と一致していることを示します。
解釈
- P-value ≤ α: 観測データは期待値と統計的に異なる(H0却下)
- p値が有意水準以下の場合は、帰無仮説を棄却し、データは特定の比率の分布に従わないと結論付けます。専門知識に基づいて、差が実際に有意かどうかを判断します。
- P-value > α: 観測データが期待値と統計的に異なると結論付けできない(H0却下失敗)
- p値が有意水準より大きい場合は、データは特定比率の分布に従わないと結論付けるだけの十分な証拠がないため、帰無仮説の棄却に失敗します。ただし、分布が同じだと結論付けることはできません。差は存在しているにもかかわらず、検定にそれを検出するのに十分な検出力がない可能性があります。
これらの結果では、p値は0.885です。p値が選択されたα値0.05より大きいため、帰無仮説を棄却することはできません。したがって、観測比率が特定の比率と有意に異なると結論付けることはできません。
カイ二乗検定
| N | 自由度 | カイ二乗 | p値 |
|---|---|---|---|
| 225 | 3 | 0.648148 | 0.885 |
