目的の方法または計算式を選択してください。
このトピックの内容
平均(正規)
標準偏差が既知の場合
母標準偏差が既知の場合、正規分布からの平均の信頼区間は、次の式で求められます。

誤差幅は次の式で求められます。
nの解は次の式で求められます。

標準偏差が未知の場合
母標準偏差が未知の場合、正規分布からの平均の信頼区間は、次の式で求められます。
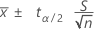
誤差幅は次の式で求められます。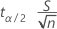
nの解を求めるには、次のような最小のnを計算します。
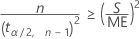
表記
| 用語 | 説明 |
|---|---|
 | サンプル平均 |
| zα/2 | 標準正規分布の1-α/2における逆累積確率。ここで、α = 1 - 信頼水準/100 |
| σ | 母集団標準偏差(既知と仮定する) |
| n | サンプルサイズ |
| ME | 誤差幅 |
| t α/2 | 自由度がn-1のt分布の1-α/2における逆累積確率 |
| S | 計画値 |
比率 (二項)
下側限界
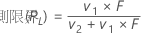
上側限界
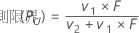
間隔(PL、PU)は、pの近似的な100(1 – α)%信頼区間です。
注
nを解くには、次のようにnの最小値を計算します:
(P – PL) ≤ MEおよび(PU – P) ≤ ME ( P = 計画値率)
表記
| 用語 | 説明 |
|---|---|
| v1(下側限界) | 2x |
| v2(下側限界) | 2(n – x + 1) |
| v1(上側限界) | 2(x + 1) |
| v2(上側限界) | 2(n – x) |
| x | 事象数 |
| n | 試行回数 |
| F(下側限界) | 自由度がv1およびv2のF分布の下限α/2の点 |
| F(上側限界) | 自由度がv1およびv2のF分布の上限α/2の点 |
率と平均(ポアソン)
計算式
ポアソン分布の率または平均に対する下側信頼限界は、次の式で求められます。
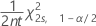
ポアソン分布の率または平均に対する上側信頼限界は、次の式で求められます。
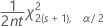
下側誤差幅は、−1×(下側信頼限界)です。上側誤差幅は、上側信頼限界に等しくなります。
nの解を求めるには、次のような最小のnを計算します。
(S – SL) ≤ MEおよび(SU – S) ≤ ME
表記
| 用語 | 説明 |
|---|---|
| n | サンプルサイズ |
| t | 観測の長さ。ポアソン平均の場合、長さ=1 |
| s | ポアソン工程での出現総数 |
| χ2p, x | 自由度pのカイ二乗分布のx番目の上位百分位数点。ここで、0 < x < 1 |
| S | 計画値 |
| ME | 誤差幅 |
分散と標準偏差(正規)
計算式
正規分布の分散に対する下側信頼限界は、次の式で求められます。
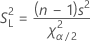
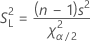
正規分布の分散に対する上側信頼限界は、次の式で求められます。
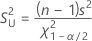
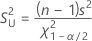
標準偏差の信頼区間は、上の式の平方根を取ることにより求められます。
下側誤差幅は、−1×(下側信頼限界)です。上側誤差幅は、上側信頼限界に等しくなります。
分散に対するnの解を求めるには、次のような最小のnを計算します。
(S2 – S2L) ≤ MEおよび(S2U – S2) ≤ ME
標準偏差に対するnの解を求めるには、次のような最小のnを計算します。
(S – SL) ≤ MEおよび(SU – S) ≤ ME
表記
| 用語 | 説明 |
|---|---|
| n | サンプルサイズ |
| s2 | サンプル分散 |
| Χ2 p | 自由度(n – 1)のカイ二乗分布の100p番目の上位百分位数点 |
| S | 計画値 |
| ME | 誤差幅 |
