パラメータ
このパラメータは、ダイアログで選択した統計量を示します。パラメータは、分布曲線を生成するために確率分布関数(PDF)の入力に使用される母集団全体の記述的測度です。パラメータ、パラメータ推定値、およびサンプル分布とは
観測の長さ
ポアソン工程では、時間、領域、量、項目数など指定された観測範囲にわたって特定の事象の発生数を数えます。観測の長さは、各観測範囲の規模、期間、またはサイズを表します。
解釈
Minitabでは、観測の長さを使用して、出現率を各自の状況に最適な形式に変換します。
たとえば、各サンプル観測値が1年間の事象数であれば、長さ1は年間の出現率を表し、長さ12は月間の出現率を表します。
- 検査者が122か所の欠陥を見つけたため、出現総数は122です。
- 検査者が50箱を抽出したため、サンプルサイズ(N)は50です。
- 各箱に10枚のタオルが入っているため、タオル1枚あたりの欠陥数を特定するには、観測の長さに10を使用します。1箱あたりの欠陥数を特定するには、観測の長さに1を使用します。
- 出現率は、(出現総数/N) / (観測の長さ) = (122/50) / 10 = 0.244となります。したがって、平均では各タオルに0.244か所の欠陥があります。
分布
- 正規
-
正規分布とは、平均からの一連の標準偏差によってデータ観測値の割合を推定するベンチマークが確立されるつりがね型の分布です。これらのベンチマークに基づいて、Z検定やt検定などの多くの仮説検定が行われます。
たとえば、ペンシルバニア州に居住するすべての成人男子の身長は、正規分布におおよそ従っています。したがって、大半の男性の身長が平均身長である69インチに近いといえます。69インチよりも身長が若干高い男性と若干低い男性の人数はほぼ同じです。身長が非常に高い男性や非常に低い男性はわずかです。
- 二項
-
物、事象、または人を独立して2つのカテゴリのどちらかに分類する場合、片方のカテゴリの物、事象、または人の数は二項分布に従います。2つのカテゴリは、はい/いいえ、合格/不合格、良/不良など、互いに排反する必要があります。
たとえば、エンジニアが、サンプルを抽出し、重大な亀裂のために使用不能なボルトがないか調べます。亀裂がないボルトは良品で、亀裂があるボルトは不良品です。
- ポアソン
-
一定の期間、領域、またはその他の観測値の長さにわたって、特性、結果、または活動の存在を数える場合、ポアソンデータが得られます。ポアソンデータは、同じサイズの単位あたりの数で評価されます。
たとえば、あるバス会社の検査者が、30日間にわたって毎日、故障したバスの台数を数えます。
標準偏差
標準偏差とは、散布度、つまり平均からのデータの広がり方を表す最も一般的な尺度です。記号σ(シグマ)は、母標準偏差を示す場合によく使用され、sはサンプルの標準偏差を示す場合に使用されます。多くの場合、工程に対してランダム(自然)な変動は雑音と呼ばれます。Minitabで表示される値は、ダイアログで指定した計画値です。
比率
比率とは、計数または度数ではなく、全体に対する相対量です。比率は、事象数をサンプルサイズで割ったものです。Minitabで表示される値は、ダイアログで指定した計画値です。
率
出現率とは、観測値の単位長さあたりに出現する事象数の平均値です。Minitabで表示される値は、ダイアログで指定した計画値です。
平均
ポアソン平均は、観察空間全体にわたる事象の平均発生数です。Minitabで表示される値は、ダイアログで指定した計画値です。
信頼水準
通常は95%の信頼水準が適切です。この水準は、同じ母集団から抽出した20個のサンプルのうち19個(95%)で母集団パラメータを含む信頼区間を得られることを示しています。
信頼水準は、同じ母集団からサンプルを繰り返し抽出する場合に母集団パラメータが含まれる区間のパーセントを表します。したがって、100個のサンプルを収集し、100個の95%信頼区間を作成した場合、次の図に示すように、その区間の約95個に母平均などの母集団パラメータが含まれることが予測されます。
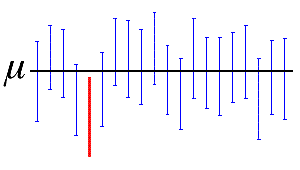
この図では、水平線は不明な母平均µの固定値を表します。水平線に重なる19個の青の垂直信頼区間には、母平均の値が含まれます。水平線とは重ならず下にある1つの赤の信頼区間にはこの値は含まれません。
信頼区間
ダイアログで指定した信頼区間のタイプが表示されます。
信頼区間は、母比率値の含まれる可能性が高い範囲です。サンプルはランダムであるため、母集団からの2つのサンプルの信頼区間が同一である可能性は低くなります。しかし、サンプルを何度も繰り返して測定すると、得られた信頼区間または限界の一定の割合には未知の母集団パラメータが含まれることになります。このようなパラメータを含む信頼区間または限界の割合(%)を区間の信頼水準と言います。
上限は、母集団パラメータがそれより小さくなる可能性が高い値です。下限は、母集団パラメータがそれより大きくなる可能性が高い値です。
