有意水準(α)
有意水準(アルファまたはαと表されます)は、タイプIの誤りのリスクの最大許容水準です。
解釈
有意水準を使用して、効果が統計的に有意であるかどうかを決定します。有意水準は統計的有意性のしきい値であるため、値が高いほどタイプIの誤りを犯す可能性が高くなります。タイプIの誤りとは、効果が統計的に有意であると誤って結論付けることです。
仮定された標準偏差
仮定された標準偏差とは、反復実験実行での応答測定値の標準偏差の推定値です。すでにMinitabで分散分析表が生成される分析を実行済みである場合、誤差の調整済み平均平方の平方根を使用できます。
解釈
仮定された標準偏差を使用して、データの変動を説明します。仮定された標準偏差の値が高いほど、データの変動または「雑音」が大きいことを示し、計画の検出力は低くなります。
因子
この数字は、計画内の因子数を示します。
解釈
因子数を使用して、分析する必要がある因子がすべて計画に含まれていることを確認します。因子とは、実験で制御する変数のことです。因子は独立変数、説明変数、および予測変数とも呼ばれます。検出力とサンプルサイズの計算では、すべての因子は数値です。数値因子に多くの値が可能であっても、実験ではいくつかの制御された値が使用されます。これらの値は因子水準と呼ばれます。
たとえば、プラスチックの製造過程において、プラスチックの強度に影響を与える可能性のある要因を研究しているとします。実験に温度を含めることにします。温度は因子であるため、実験では100°C、150°C、200°Cの3つの温度設定のみを使用します。
基本計画
数字は、基本計画の因子の数と頂点の数を示します。
解釈
基本計画を使用して、実験計画が完全実施計画であるか一部実施計画であるかを決定します。頂点の数が2^(因子数)よりも小さい場合は、実験計画は一部実施計画です。一部実施計画では、計画で推定できる項のすべてがお互いに独立しているわけではありません。項がお互いにどのように依存しているかを調べるには、計画を作成し、交絡表を確認します。
基本計画は、最終計画作成の開始点です。基本計画に項目を追加することにより、異なる目的を達成できます。たとえば、反復数や中心点を追加することにより、計画の検出力を高めることができます。
ブロック
数字は、計画内のブロックの数を示しています。
解釈
ブロック数を使用して、検出力の計算で使用される計画を識別します。ブロックは比較的均一な条件下で実行される実験の実行グループです。各観測値は(実験の一部として実験条件が変わる場合を除き)一貫した実験条件で測定する必要がありますが、それが不可能な場合もあります。
たとえば、新しい印刷機の品質を試験するとします。しかし、印刷機の設定には数時間かかり、1日に4回しか行うことができません。実験計画では少なくとも8回実行する必要があるので、印刷機を試験するには最低2日は必要です。「日」をブロック変数として使用して、実験日による条件の違いを説明する必要があります。ブロック効果(実験日間の偶発的な差)と実験因子(温度、湿度、印刷機のオペレータなど)による効果を区別するため、実験計画でブロック(日)について説明する必要があります。ブロック内の実行順序はランダム化する必要があります。Minitabで実行をブロックに割り当てる方法についての詳細は、ブロックとはを参照してください。
ブロックあたりの中心点数
この数字は、計画内のブロックあたりの中心点数を示します。
解釈
ブロックあたりの中心点数を使用して、検出力の計算で使用する計画を特定します。中心点とは、すべての因子が低水準と高水準の中間に設定されている実行です。計画にブロックが含まれる場合、Minitabでは各ブロックに同じ数の中心点が追加されます。たとえば、ブロックあたりの中心点数を2、ブロック数を2と指定すると、計画には4個の中心点が含まれます。
通常、計画に中心点の反復が含まれる場合、中心点が結果に及ぼす影響は小さくなります。中心点には、検出力の計算に及ぼす影響以外の用途があります。たとえば、応答の曲面性の検定には中心点が必要です。
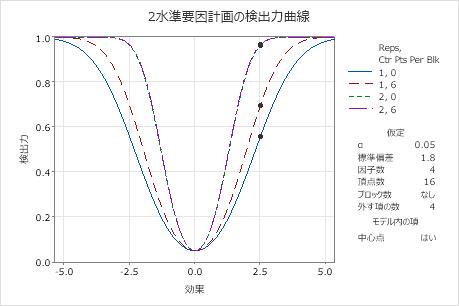
これらの結果では、検出力曲線上の点は、2.5の差に対する計算を示しています。反復が1回で中心点がない計画の検出力はおよそ0.56です。反復が1回で6つの中心点がある計画の検出力はほとんど0.7になっています。反復数が2の場合、中心点数が0と6の検出力曲線は、グラフ上で区別がつきません。中心点が6つの曲線は非ゼロ効果のため、わずかに高くなっています。いずれも検出力値は0.95を超えています。
方法
| 因子: | 4 | 基本計画: | 4, 16 |
|---|---|---|---|
| ブロック: | なし |
結果
| 中心点 | 効果 | 反復 | 全実行数 | 検出力 |
|---|---|---|---|---|
| 0 | 2.5 | 1 | 16 | 0.557255 |
| 0 | 2.5 | 2 | 32 | 0.961939 |
| 6 | 2.5 | 1 | 22 | 0.696490 |
| 6 | 2.5 | 2 | 38 | 0.965121 |
効果
反復数、検出力値、および中心点数を入力すると、効果が計算されます。効果とは、計画で検出する因子の高水準と低水準の応答間の差のことです。この差は1つの因子のみ(主効果)の結果です。
解釈
効果サイズを使用して、計画が効果を検出できる能力を決定します。反復数、検出力、および中心点数を入力すると、計画によって指定した検出力で検出できる最小の効果サイズが計算されます。通常、反復数が増えるほど、小さな効果を計画実験によって検出できます。
これらの結果では、反復が1回の計画では約0.015の差を80%の検出力で検出できます。90%の検出力で検出できる差は0.015より大きく、約0.018です。反復が2回の計画では、80%の検出力で0.015より小さい約0.007の差を検出できます。
方法
| 因子: | 5 | 基本計画: | 5, 32 |
|---|---|---|---|
| ブロック: | なし |
結果
| 中心点 | 反復 | 全実行数 | 検出力 | 効果 |
|---|---|---|---|---|
| 4 | 1 | 36 | 0.8 | 0.0153027 |
| 4 | 1 | 36 | 0.9 | 0.0180278 |
| 4 | 2 | 68 | 0.8 | 0.0073261 |
| 4 | 2 | 68 | 0.9 | 0.0084775 |
反復数
反復とは、同じ因子設定で実験を複数回実行することです。
解釈
反復数を使用して、計画に含める実験実行数を推定します。検出力、効果サイズ、および中心点数を入力すると、反復数が計算されます。反復数と中心点は整数値で与えられるため、実際の検出力はわずかに目標値より大きい値になる場合があります。反復数を増やすと、計画の検出力も高まります。適切な検出力を達成するには、反復数が十分である必要があります。
反復数は整数値であるため、指定する検出力値は目標の検出力値です。実際の検出力値は、計画実験の反復数と中心点数に対応する値です。実際の検出力値は目標の検出力値以上になります。
これらの結果では、目標検出力を達成するための反復数が計算されています。検出力0.8で、2の効果を検出する計画には1回の反復が必要です。検出力0.9を達成するには、計画に2回の反復が必要です。2回の反復での実際の検出力は0.99よりも大きくなります。この実際の検出力は、整数の反復数によって達成できる、0.9以上の最も小さい検出力の値です。検出力0.8で、小さい方の0.9の効果を検出するには、計画に4回の反復が必要です。検出力0.9で、小さい方の0.9の効果を検出するには、計画に5回の反復が必要です。
方法
| 因子: | 15 | 基本計画: | 15, 32 |
|---|---|---|---|
| ブロック: | なし |
結果
| 中心点 | 効果 | 反復 | 全実行数 | 目標検出力 | 実際の検出力 |
|---|---|---|---|---|---|
| 0 | 2.0 | 1 | 32 | 0.8 | 0.877445 |
| 0 | 2.0 | 2 | 64 | 0.9 | 0.995974 |
| 0 | 0.9 | 4 | 128 | 0.8 | 0.843529 |
| 0 | 0.9 | 5 | 160 | 0.9 | 0.914018 |
最初の結果セットを2番目の結果セットと比較します。最初の結果セットでは、モデルから16個の項が除外されています。2番目の結果セットでは、すべての推定可能な項がモデルに含まれています。2番目のモデルは計画の単一の反復にすべての自由度を使用するため、解として1回の反復は含まれません。モデル内の項の数がより多いため、その他の検出力値は、項が除外されるモデルでの結果よりも低くなります。たとえば、反復数が5の計画の実際の検出力は、最初の結果セットでは約0.9140で、2番目の結果セットでは約0.9136です。
方法
| 因子: | 15 | 基本計画: | 15, 32 |
|---|---|---|---|
| ブロック: | なし |
結果
| 中心点 | 効果 | 反復 | 全実行数 | 目標検出力 | 実際の検出力 |
|---|---|---|---|---|---|
| 0 | 2.0 | 2 | 64 | 0.8 | 0.995347 |
| 0 | 2.0 | 2 | 64 | 0.9 | 0.995347 |
| 0 | 0.9 | 4 | 128 | 0.8 | 0.842492 |
| 0 | 0.9 | 5 | 160 | 0.9 | 0.913575 |
全実行数
実験の実行とは、応答を測定する因子水準の組み合わせのことです。実行の合計数は、計画内の応答の測定値数です。同じ因子水準の組み合わせで行われる複数回の実行は、それぞれ別の実験実行とみなされ、反復と呼ばれます。
解釈
全実行数を使用して、計画実験がリソースに対して適切なサイズであることを確認します。2水準要因計画の場合、次の計算式により実験の全実行数が求められます。

| 用語 | 説明 |
|---|---|
| n | 反復数 |
| r | 反復あたりの頂点数 |
| cpblock | ブロックあたりの中心点数 |
| b | ブロック数 |
これらの結果では、基本計画には16個の頂点があります。この計画には4つのブロックがあり、ブロックあたり4つの中心点があるため、合計で4*4 = 16個の中心点があります。したがって、1回の反復の計画には、16個の頂点と16個の中心点があり、実験の全実行数は16 + 16 = 32回となります。2回の反復の計画では、頂点の数は倍の2*16 = 32個となります。ブロック数とブロックあたりの中心点数はそのままです。その結果、2回の反復の計画の全実行数は32 + 16 = 48回となります。
方法
| 因子: | 4 | 基本計画: | 4, 16 |
|---|---|---|---|
| ブロック: | 4 |
結果
| ブロックあ たりの中心 点のラン数 | 効果 | 反復 | 全実行数 | 検出力 |
|---|---|---|---|---|
| 4 | 2.5 | 1 | 32 | 0.741569 |
| 4 | 2.5 | 2 | 48 | 0.967699 |
検出力
計画の検出力とは、計画によって効果が統計的に有意であると結論付けられる可能性です。因子の高水準と低水準の応答変数の平均間の差が効果サイズです。
解釈
検出力の値を使用して、計画が効果を検出する能力を判定します。反復回数、効果量、中心点数を入力すると、Minitabでは、計画の検出力が計算されます。検出力は通常、0.9で十分だと考えられます。0.9という値は、計画が指定する大きさの効果を90%の確率で検出できることを示します。通常、反復回数が少ないほど、検出力は弱くなります。計画の検出力が低い場合は、効果を検出できず、何も存在しないという誤った結論を出してしまう可能性があります。
これらの結果により、実験実行回数が増えるといかに検出力が上がるのかがわかります。効果量0.9の場合、計画の検出力は総実行回数64回でおよそ0.55です。総実行回数160回だと、計画の検出力はおよそ0.91まで高まります。
これらの結果により、効果量が増えるといかに検出力が上がるのかもわかります。64回実行の計画の場合、検出力は効果量0.9でおよそ0.55です。効果量1.5だと、検出力はおよそ0.93まで高まります。
方法
| 因子: | 15 | 基本計画: | 15, 32 |
|---|---|---|---|
| ブロック: | なし |
結果
| 中心点 | 効果 | 反復 | 全実行数 | 検出力 |
|---|---|---|---|---|
| 0 | 1.5 | 5 | 160 | 0.999830 |
| 0 | 1.5 | 2 | 64 | 0.932932 |
| 0 | 0.9 | 5 | 160 | 0.914018 |
| 0 | 0.9 | 2 | 64 | 0.545887 |
検出力曲線
この検出力曲線では、計画の検出力と効果のサイズが対比されてプロットされます。効果とは、因子の高水準と低水準の平均応答値の差です。
解釈
検出力曲線を使用して、計画に適したプロパティを評価します。
この検出力曲線は、中心点と反復のすべての組み合わせに対する検出力と効果サイズの関係を表します。検出力曲線上の記号は、入力したプロパティに基づいて計算された値を表します。たとえば、反復数、検出力値、および中心点の数を入力すると、それに対応する効果サイズが計算され、反復と中心点の組み合わせに対するグラフ上に、計算された値が表示されます。反復と中心点を計算する場合、プロットには、目標の検出力を達成するその他の反復と中心点の組み合わせに対する曲線も含まれます。プロットには、統計的有意性を評価するのに十分な自由度がない場合に対する曲線は表示されません。
曲線上の値を調べることにより、特定の検出力値、頂点の数、および中心点の数において実験で検出できる効果サイズを決定できます。通常、検出力の値として0.9は適切であるとされます。ただし、分析者によっては、検出力の値として0.8が適切であると考えることもあります。計画の検出力が低い場合、実際には有意である効果を検出できない可能性があります。反復数を増やすと、計画の検出力が高まります。適切な検出力を達成するには、計画内の実験の実行数が十分である必要があります。小さな効果よりも大きな効果を検出する方が、計画の検出力が高くなります。
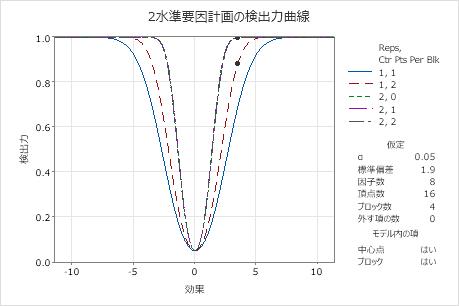
これらの結果では、効果サイズ3.5に対して目標検出力0.8または0.9以上を達成するための反復数が計算されています。計画実験には、4つの因子を調べるために4つのブロックに16個の頂点があります。計算では、ブロックごとの中心点数が0、1、または2の計画実験について考慮します。反復数が1で中心点数が2の曲線では、検出力が目標検出力の0.8より高い位置に効果が3.5であることを示す記号があります。反復数が2の実験を表す3つの曲線には、3.5の効果を検出するための検出力が目標検出力の0.9を超えていることを示す記号があります。
反復数が2で中心点数が1の解と反復数が1で中心点数が2の解が存在するため、プロットには反復数が1で中心点数が1の実験の曲線も含まれます。この実験では、3.5の効果に対して目標の検出力はいずれも達成されていないため、この曲線上には記号がありません。プロットには反復数が1で中心点数が0の曲線は含まれていません。これは、この実験には、モデルから0個の項が除外されたときに統計的優位性を評価するのに十分な自由度がないためです。
