目的の方法または計算式を選択してください。
Leveneの方法による検出力の計算
分散検定の検出力関数は、Q(ρ) = P(H0を棄却 | ρ)です。
片側検出力(H1: σ1 / σ2 < 1
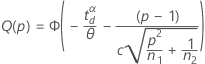
片側検出力(H1: σ1 / σ2 > 1)
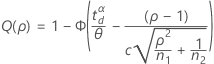
両側検出力(H1: σ1 / σ2 ≠ 1
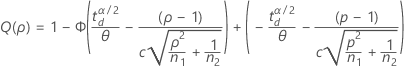
表記
| 用語 | 説明 |
|---|---|
| Φ | 標準正規分布の累積分布関数 |
| tα d | 自由度がd = n1 + n2 – 2のt分布の上位百分位数点 |
| θ | 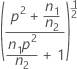 |
| c |  |
| ρ | σ1 / σ2 |
| n 1 | 第1サンプルサイズ |
| n 2 | 第2サンプルサイズ |
F検定法による検出力の計算
計算式
分散検定の検出力関数は、Q(ρ) = P(H0を棄却 | ρ)です。
片側検出力(H1: σ1 / σ2 < 1)
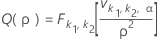
片側検出力(H1: σ1 / σ2 > 1)
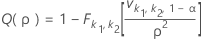
両側検出力(H1: σ1 / σ2 ≠ 1)
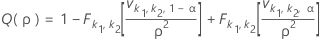
表記
| 用語 | 説明 |
|---|---|
| F k 1, k 2 | 自由度k1およびk2のF分布の分布関数 |
| v k 1, k 2, A | 自由度k1およびk2のF分布の逆累積分布関数をAの位置で評価したもの |
| k1 | n – 1 |
| k2 | n – 1 |
| α | 有意水準 |
| ρ | σ1 / σ2 |
Bonettの方法による検出力の計算
注
Bonettの方法の検出力を計算するには、セッションコマンドのPOWERを、サブコマンドTWOVARIANCEおよびBONETTと共に使用します。
分散検定の検出力関数は、Q(ρ) = P(H0を棄却 | ρ)です。Bonettの検定の場合、検出力関数の計算は統計量Zに基づいています。サンプルがより大きくなると、Zはほぼ標準正規分布に従います。Zは次の式で求められます。
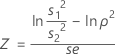
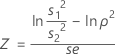
ここで、seは標準誤差で、次の式で求められます。


片側検出力(H1: σ1 / σ2 < 1)
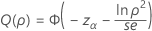
片側検出力(H1: σ1 / σ2 > 1)
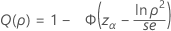
片側検出力(H1: σ1 / σ2 ≠ 1)

表記
| 用語 | 説明 |
|---|---|
| Si | サンプルiの標準偏差 |
| ρ | 母標準偏差の比(s1 / s2) |
| se | 標準誤差 |
| γ | 母集団の真の共通尖度(γは過剰尖度ではありません) |
| n | サンプルサイズ(検出力の計算では、nは両方のサンプルで同じであると仮定します) |
| Φ | 標準正規分布の累積分布関数 |
| α | 検定の有意水準 |
| zi | 標準正規分布のi番目の上側百分位数点 |
サンプルサイズと比の計算
検出力とサンプルサイズの値を指定すると、比の値が計算されます。検出力と比の値を指定すると、サンプルサイズが計算されます。
これらの2つの場合では、検出力の式と繰り返しアルゴリズムが使用されます。各繰り返しのたびに、試行サンプルサイズまたは試行比に対する検出力が評価され、それが指定した値に達すると停止します。
目標検出力と実際の検出力
サンプルサイズを計算するとき、目標検出力になるサンプルサイズの整数値がない場合があります。そのような場合は、検出力の目標値と実際の検出力が併せて表示されます。実際の検出力は、整数のサンプルサイズに対応する値で、目標値より大きく目標値に最も近い値です。
