このトピックの内容
ステップ1:計算値を調査
Minitabでは、入力した2つの検出力関数変数の値が用いられ、比、サンプルサイズ、検定の検出力が計算されます。
- 比
-
Minitabでは、指定した検出力とサンプルサイズに基づいて検出可能な、最小比が計算されます。サンプルサイズが大きいほど、小さな比を検出できるようになります。応用に実際的な影響を与える最小比を検出したいとします。
- サンプルサイズ
-
Minitabでは、指定した比を検出するためにどれぐらいの大きさのサンプルが指定した検出力に必要なのかが、計算されます。サンプルサイズは整数であるため、検定の実際の検出力は、指定した検出力値よりわずかに大きいかもしれません。
サンプルサイズを大きくすると、検定の検出力も高まります。十分な検出力に到達できるよう、サンプルに十分な観測値がほしいところです。ですが、サンプルサイズを大きくして、不要な抽出で時間とお金を無駄にし、重要ではない差を統計的に優位に検出したりしたくはありません。
- 検出力
-
Minitabでは、指定した比とサンプルサイズに基づいて、検定の検出力が計算されます。検出力は通常、0.9で十分だと考えられます。値0.9は、差が実際に存在する場合に、母集団比較標準偏差または分散と仮説標準偏差または分散の差を検出できる確率が90%であることを示します。検定の検出力が低いと、差を検出できず、差は存在しないと誤って結論付けてしまう可能性があります。通常、サンプルサイズが小さいまたは比が1に近い場合、検定の差に対する検出力は弱くなります。
注
基本統計で1サンプルの分散を実行すると、カイニ乗方法とボネット方法の両方の結果が表示されます。ただし、1分散の検出力とサンプルサイズを実行する場合は、カイニ乗方法しか使用されません。
結果
| 比 | サンプルサイズ | 検出力 |
|---|---|---|
| 0.8 | 50 | 0.539065 |
| 0.8 | 100 | 0.865153 |
主要な結果:差、サンプルサイズ、検出力
これらの結果の示すこととは、比が0.8、サンプルサイズが50、100の場合、検定の検出力は各サンプルサイズでそれぞれ約0.54、0.87だということです。0.87は0.9に近いため、サンプルサイズ100を使用することにより、比率0.8で十分な検出力を得られます。
ステップ2: 検出力曲線を調べる
検出力曲線を使用して、検定に適したサンプルサイズと検出力を評価します。
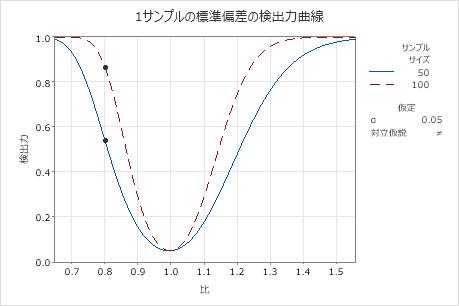
この検出力曲線は、有意水準を一定に保って、各サンプルサイズに対する検出力と比のすべての組み合わせを表します。検出力曲線上の記号は、入力した値に基づいて計算された値を表します。たとえば、サンプルサイズと検出力の値を入力すると、それに対応する比が計算され、計算された値がグラフ上に表示されます。
曲線上の値を調べることにより、特定の検出力値とサンプルサイズにおいて検出できる比を決定できます。通常、検出力の値として0.9は適切であるとされます。ただし、分析者によっては、検出力の値として0.8が適切であると考えることもあります。仮説検定の検出力が低い場合、実際には有意である比を検出できない可能性があります。サンプルサイズを大きくすると、検定の検出力も高くなります。適切な検出力を達成するには、サンプル内の観測値数が十分である必要があります。しかし、サンプルサイズを大きくしすぎて、不必要なサンプリングに時間と費用を浪費したり、統計的に有意な重要でない差を検出することは望ましくありません。検出する比のサイズを小さくすると、検出力も低くなります。
注
基本統計で1サンプルの分散を実行すると、カイニ乗方法とボネット方法の両方の結果が表示されます。ただし、1分散の検出力とサンプルサイズを実行する場合は、カイニ乗方法しか使用されません。
このグラフでは、サンプルサイズ50の検出力曲線は、約0.54の差に対して検定の検出力が0.8であることを示しています。サンプルサイズ100の検出力曲線は、約0.87の差に対して検定の検出力が0.8であることを示しています。0.87の検出力が状況に対して十分である場合は、100のサンプルサイズを収集します。0.8より小さい比を検出する必要がある場合は、より大きなサンプルサイズを収集する必要があります。