α(アルファ)
有意水準(αまたはアルファと表されます)は、帰無仮説が真であるときにその帰無仮説を棄却する(タイプIの誤り)のリスクの最大許容水準です。また、αは、帰無仮説(H0)が真の場合の検定の検出力とも解釈できます。通常、データを分析する前に有意水準を選択します。デフォルトの有意水準は0.05です。
解釈
有意水準を使用して、帰無仮説(H0)が真の場合の検定の検出力値を最小化します。有意水準の値が高いほど、検定の検出力が高くなりますが、真である帰無仮説を棄却してしまうタイプIの誤りを犯す可能性も高くなります。
仮定された標準偏差
標準偏差とは、散布度、つまり平均に対するデータの変動を表す最も一般的な尺度です。多くの場合、工程に対してランダム(自然)な変動は雑音と呼ばれます。
解釈
仮定された標準偏差とは、検出力分析のために入力する母標準偏差の計画推定値です。Minitabでは、検定の検出力を計算するために、仮定された標準偏差が使用されます。標準偏差の値が高いほど、データの変動が大きいことを示し、検定の検出力は低くなります。差
この値は、実際の母平均と仮説の平均との差を表します。
解釈
各サンプルサイズに対して、指定した水準の検定力を達成できる最小の差が計算されます。サンプルサイズが大きくなるほど、小さな差を検出できます。用途に対して実質的に影響のある最小の差を検出できるようにする必要があります。
サンプルサイズと、指定された検出力における差の関係をより詳しく調べるには、検出力曲線を使用します。
サンプルサイズ
サンプルサイズとは、サンプルに含まれる観測値の合計数のことです。
解釈
サンプルサイズを使用して、仮説検定において、特定の差で特定の検出力値を得るために必要な観測値数を推定します。
指定したそれぞれの差を検出するために、指定した検出力の検定に必要なサンプルサイズが計算されます。サンプルサイズは整数であるため、検定の実際の検出力は、指定した検出力値よりもわずかに大きくなる場合があります。
サンプルサイズを大きくすると、検定の検出力も高くなります。適切な検出力を達成するには、サンプル内の観測値数が十分である必要があります。しかし、サンプルサイズを大きくしすぎて、不必要なサンプリングに時間と費用を浪費したり、重要でない差が統計的に有意であることを検出することは望ましくありません。
サンプルサイズと、指定された検出力における差の関係をより詳しく調べるには、検出力曲線を使用します。
検出力
仮説検定の検出力は、検定で帰無仮説が正しく棄却される確率です。仮説検定の検出力は、サンプルサイズ、差、データの変動性、検定の有意水準に影響されます。
詳細は、検出力とはを参照してください。
解釈
Minitabでは、特定の差と標本の大きさに基づいて、検定の検出力が計算されます。検出力は通常、0.9で十分だと考えられます。0.9という値は、母平均と目標の差が存在する場合に、母平均と目標の差を90%の確率で検出できることを示します。検定の検出力が弱い場合、差を検出できず、何も存在しないという誤った結論を出す可能性があります。通常、標本の大きさまたは差が小さいほど、検定の差の検出力は弱くなります。
検定での差と検出力値を入力すると、必要なサンプルサイズが計算されます。Minitabでは、そのサンプルサイズで検定を行う場合の実際の検出力も計算されます。サンプルサイズは整数であるため、検定の実際の検出力は、指定した検出力値よりもわずかに大きくなる場合があります。
検出力曲線
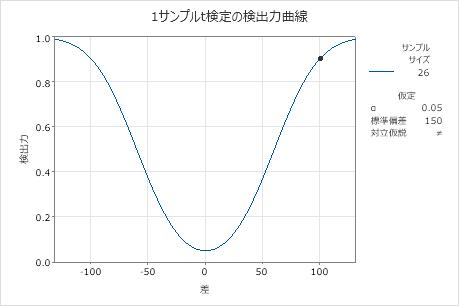
この検出力曲線では、検定の検出力に対して平均と目標値の間の差がプロットされます。
解釈
検出力曲線を使用して、検定に適したサンプルサイズと検出力を評価します。
この検出力曲線は、有意水準と標準偏差を一定に保って、各サンプルサイズに対する検出力と差のすべての組み合わせを表します。検出力曲線上の記号は、入力した値に基づいて計算された値を表します。たとえば、サンプルサイズと検出力の値を入力すると、それに対応する差が計算され、計算された値がグラフ上に表示されます。
曲線上の値を調べることにより、特定の検出力値とサンプルサイズにおいて検出できる平均と目標の差を決定できます。通常、検出力の値として0.9は適切であるとされます。ただし、分析者によっては、検出力の値として0.8が適切であると考えることもあります。仮説検定の検出力が低い場合、実際には有意である差を検出できない可能性があります。サンプルサイズを大きくすると、検定の検出力も高くなります。適切な検出力を達成するには、サンプル内の観測値数が十分である必要があります。しかし、サンプルサイズを大きくしすぎて、不必要なサンプリングに時間と費用を浪費したり、統計的に有意な重要でない差を検出することは望ましくありません。検出する差のサイズを小さくすると、検出力も低くなります。
このグラフでは、サンプルサイズ26の検出力曲線は、100の差に対して検定の検出力が0.9であることを示しています。差が0に近づくにつれて、検定の検出力は低下し、α(有意水準とも呼ばれます)に近づきます。αはこの分析では0.05です。