ある包装エンジニアは、スナック袋を密封する新しい方法をテストしたいと考えています。袋を開けるために必要な力は目標値4.2N(ニュートン)の10%以内に収まる必要があります。 エンジニアは、1サンプル同等性検定のためのデータを収集する前に、検出力とサンプルサイズの計算によって、検定で検出力80%(0.8)を得るために必要なサンプルサイズを調べます。以前のサンプルから、エンジニアは母集団の標準偏差が0.332であると推定します。
- を選択します。
- 何を判定しますか? (対立仮説)から下側限界 < 検定平均値 - 目標値 < 上側限界を選択します。
- 下側限界に「–0.42」と入力します。上側限界に「0.42」と入力します。
- 差(制限内)に「0 0.1 0.2 0.3」と入力します。
- 検出力に「0.8」と入力します。
- 標準偏差に「0.332」と入力します。
- OKをクリックします。
結果を解釈する
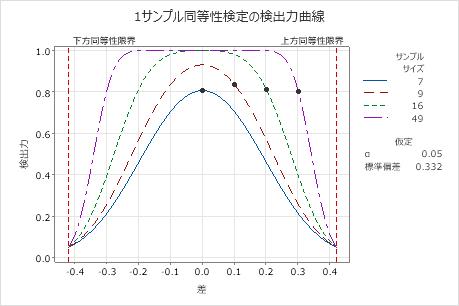
差が0(平均の力が目標値に達している)の場合、0.8の検出力を達成するために必要なサンプルサイズは7です。サンプルサイズに9を使用すると、0の差に対する検定の検出力は0.9を超えます。
差が上側同等性限界(0.42)に近くなると、同じ検出力を達成するために、より大きなサンプルサイズが必要になります。たとえば、差が0.3の場合、検出力0.8を達成するには49のサンプルサイズが必要です。
あらゆるサンプルサイズで、差が下側同等性限界または上側同等性限界に近づくにつれて、検定の検出力は低下し、α(アルファ。同等でない場合に同等であるとするリスク)に近づきます。
方法
| 差に対する検出力: | 検定平均値 - 目標値 |
|---|---|
| 帰無仮説: | -0.42以下または0.42以上の差 |
| 対立仮説: | -0.42 < 差 < 0.42 |
| α水準: | 0.05 |
| 仮定された標準偏差: | 0.332 |
結果
| 差 | サンプルサイズ | 目標検出力 | 実際の検出力 |
|---|---|---|---|
| 0.0 | 7 | 0.8 | 0.805075 |
| 0.1 | 9 | 0.8 | 0.834590 |
| 0.2 | 16 | 0.8 | 0.811465 |
| 0.3 | 49 | 0.8 | 0.802154 |