次の手順を実行して、連検定を解釈します。主要な出力には、観測された連の数、期待される連の数、およびp値が含まれます。
ステップ1:観測された実行数と期待される実行数の差を調べる
観測された実行数は、比較基準Kより多いかまたは少ない観測値のグループの数です。ラインはKを表します。この例には5つの実行が含まれています。
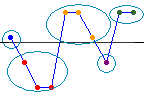

観測された実行数が期待される実行数より実質的に多いか、または少ない場合は、データの順序がランダムではない可能性が高くなります。データの順序がランダムかどうかを判断するには、p値を有意水準と比較します。
検定
| 帰無仮説 | H₀: データの順序はランダムです |
|---|---|
| 対立仮説 | H₁: データの順序はランダムではありません |
| 実行数 | ||
|---|---|---|
| 観測値 | 期待 | p値 |
| 17 | 16.77 | 0.930 |
主要な結果:観測された実行数と期待される実行数
これらの結果において、観測された実行数の値は、期待される実行数の値に非常に近くなっています。
ステップ2:データの順序がランダムかどうかを判断する
データの順序がランダムかどうかを判断するには、p値を有意水準と比較します。通常は、有意水準(αまたはアルファとも呼ばれる)として0.05が適切です。有意水準0.05は、データの順序が実際にはランダムであるのに、ランダムではないと結論づけるリスクが5%あることを示しています。
- p値 ≤ α:データの順序はランダムではない(H0を棄却)
- p値が有意水準以下の場合は、帰無仮説を棄却し、データの順序はランダムではないと結論付けます。
- p値 > α:データの順序がランダムではないとは結論付けることができない(H0を棄却できない)
- p値が有意水準よりも大きい場合は、帰無仮説を棄却しない決定を下します。この場合、データの順序がランダムではないと結論付けるのに十分な証拠がありません。
検定
| 帰無仮説 | H₀: データの順序はランダムです |
|---|---|
| 対立仮説 | H₁: データの順序はランダムではありません |
| 実行数 | ||
|---|---|---|
| 観測値 | 期待 | p値 |
| 17 | 16.77 | 0.930 |
主要な結果:p値
これらの結果において、帰無仮説ではデータの順序はランダムです。p値が0.93で、有意水準0.05より大きいため帰無仮説を棄却できません。この場合、データの順序がランダムではないと結論付けるのに十分な証拠がありません。
