連検定のすべての統計量を解釈する

連検定で使用されるすべての統計量の定義と解釈について解説します。

N

サンプルサイズ（N）は、サンプルに含まれる観測値の合計数です。サンプルサイズは、期待される実行回数およびp値に影響を与えます。

Kは比較基準の値です。デフォルトでは、Kはサンプルデータの平均です。だたし、中間値などの別の値を指定することもできます。Minitabでは、Kを使用して観測された実行数を計算します。

Kより上の観測値の数は、デフォルトの平均である比較基準の値よりも大きい観測値の数です。Kより下の観測値の数は、比較基準値以下の観測値の数です。Minitabでは、これらの値を使用してp値を計算します。

帰無仮説と対立仮説は、データ順序についての相互に排他的な2つの仮説です。仮説検定手法では、サンプルデータを用いて帰無仮説を棄却するかどうかを判断します。

観測された実行数は、比較基準Kより多いかまたは少ない観測値のグループの数です。ラインはKを表します。この例には5つの実行が含まれています。

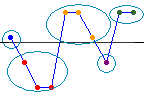
期待される実行数は、ランダム系列における実行のサンプル分布の平均です。観測された実行数が期待される実行数より実質的に多いか、または少ない場合は、データの順序がランダムではない可能性が高くなります。データの順序がランダムかどうかを判断するには、p値を有意水準と比較します。

p値は帰無仮説を棄却するための証拠を測定する確率です。確率が低いほど帰無仮説を棄却するための強力な証拠となります。

p値を使用して、データの順序がランダムかどうかを判断します。

データの順序がランダムかどうかを判断するには、p値を有意水準と比較します。通常は、0.05の有意水準（αまたはアルファとも呼ばれる）が有効に機能します。0.05の有意水準は、実際にはデータの順序がランダムであるにもかかわらず、ランダムではないと結論付ける可能性が5%であることを示しています。

p値 ≤ α：データの順序はランダムではない（H₀を棄却）: p値が有意水準以下の場合は、帰無仮説を棄却し、データの順序はランダムではないと結論付けます。
p値＞ α：データの順序がランダムではないとは結論付けることができない（H₀を棄却できない）: p値が有意水準値より大きい場合は、帰無仮説を棄却できません。この場合、データの順序がランダムではないと結論付けるのに十分な証拠がありません。