検定統計量
- Minitabにより、2つの結合されたサンプルが順位付けされます。最小観測値には順位1が、2番目に小さな観測値には順位2が割り当てられ、以下同様に順位が割り当てられます。
- 2つ以上の観測値が結合される場合は、両方の観測値に平均順位が割り当てられます。
- Minitabで最初のサンプルの順位の和が計算されます。
同順位値の順位付け
- 観測値を昇順で並べ替えます。
- 同順位が存在しなかったかのように各観測値に順位を付けます。
- 同順位セットの場合は、対応する順位の平均を求め、この値を新しい順位としてそのセットの各同順位値に割り当てます。
例
サンプルに9個の観測値（2.4、5.3、2.4、4.0、1.2、3.6、4.0、4.3、および4.0）があります。
| 観測値 | 順位
同順位なしと仮定 |
順位 | |
|---|---|---|---|
| 1.2 | 1 | 1 | |
| 同順位 | 2.4 | 2 | 2.5 |
| 2.4 | 3 | 2.5 | |
| 3.6 | 4 | 4 | |
| 同順位 | 4.0 | 5 | 6 |
| 4.0 | 6 | 6 | |
| 4.0 | 7 | 6 | |
| 4.3 | 8 | 8 | |
| 5.3 | 9 | 9 |
- 同順位セットの数は2。
- 最初のセットに含まれる同順位値の数は2。
- 2番目のセットに含まれる同順位値の数は3。
p値
計算式
Mann-Whitney検定では、正規近似法を使用して検定のp値を算定します。
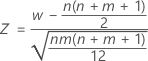は、平均値0および標準偏差1、N(0,1)のほぼ正規分布に従います。
| 対立仮説 | p値 |
|---|---|
| H1: η1 > η2 |  |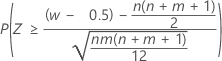
| H1: η1 < η2 |  |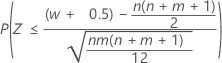
| H1: η1 ≠ η2 |  |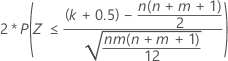
通常、調整されたp値は調整前のp値よりも正確です。ただし、未調整のp値は、特定のサンプルペアの場合に調整されたp値よりも必ず大きくなるため、より控えめな推定値となります。
表記
| 用語 | 説明 |
|---|---|
| W | Mann-Whitney検定の統計量 |
| n | サンプル1のサイズ |
| m | サンプル2のサイズ |
| η1 | サンプル1の中央値 |
| η2 | サンプル2の中央値 |
| k |  |
| i | 1、2、…、I |
| I | 同順位セットの数 |
| ti | i番目の同順位のセットに含まれる同順位値の数 |
点推定
η1 - η2の点推定を計算するためにMinitabで使用される近似アルゴリズムについては、記事「J.W. McKean and T.A. Ryan, Jr. (1977). "An Algorithm for Obtaining Confidence Intervals and Point Estimates Based on Ranks in the Two Sample Location Problem", Transactions on Mathematical Software, 183–185」で説明されています。
信頼区間
η1 - η2の信頼区間は、η1 - η2の値の範囲として定義され、この区間で帰無仮説は棄却されません。
Minitabで信頼区間の計算に使用される手法については、記事「J.W. McKean and T.A. Ryan, Jr. (1977). "An Algorithm for Obtaining Confidence Intervals and Point Estimates Based on Ranks in the Two Sample Location Problem", Transactions on Mathematical Software, pp.183-185」を参照してください。
