目的の方法または計算式を選択します。
平均順位
Minitabでは、次のようにして平均順位を計算します。
- 結合されたサンプルに順位付けし、最小観測値には順位1を、2番目に小さな観測値には順位2を割り当て、以下同様に順位を割り当てます。
- 2つ以上の観測値が結合される場合は、両方の観測値に平均順位が割り当てられます。
- 各サンプルの順位の平均が計算されます。
Minitabの出力の[平均順位]に、各グループの値が表示されます。
Z値
計算式
Minitabでは、次のようにして各グループのz値を計算します。
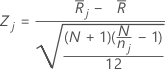
表記
| 用語 | 説明 |
|---|---|
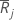 | グループjの平均順位 |
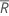 | すべての観測値の平均順位 |
| N | 観測値数 |
| nj | j番目のグループの観測値の数 |
同順位値の順位付け
同順位値は、2つ以上の観測値が等しい場合に発生します。データが同順位値の場合、Minitabでは次のようにしてデータに順位付けします。
- 観測値を昇順で並べ替えます。
- 同順位が存在しなかったかのように各観測値に順位を付けます。
- 同順位セットの場合は、対応する順位の平均を求め、この値を新しい順位としてそのセットの各同順位値に割り当てます。
例
サンプルには9個の観測値(2.4、5.3、2.4、4.0、1.2、3.6、4.0、4.3、および4.0)があります。
| 観測値 | 順位(同順位なしと仮定) | 順位 |
|---|---|---|
| 1.2 | 1 | 1 |
| 2.4 | 2 | 2.5 |
| 2.4 | 3 | 2.5 |
| 3.6 | 4 | 4 |
| 4.0 | 5 | 6 |
| 4.0 | 6 | 6 |
| 4.0 | 7 | 6 |
| 4.3 | 8 | 8 |
| 5.3 | 9 | 9 |
検定統計量の計算には次の情報も使用されます。
- 同順位セットの数 = 2
- 最初のセットに含まれる同順位値の数 = 2
- 2 番目のセットに含まれる同順位値の数 = 3
H
計算式

帰無仮説では、自由度k - 1のカイ二乗分布によってHの分布を近似します。この近似は、含まれる観測値の数が5より少ないグループが存在しない場合、ほぼ正確です。Hの値が高いほど、帰無仮説の証拠もより強力になり、いくつかの中央値間での差も十分に有意になります。
Lehmann (1975)1などの一部の著者は、データに同順位が存在する場合にはHを調製することを提案しています。
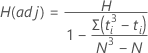
帰無仮説では、自由度がk - 1のカイ二乗分布によってHおよびH(adj)の布を近似します。
P値 = 1 – CDF (χ2H, df)
P値 = 1 – CDF (χ2H(adj), df)
サンプルが小さい場合は、正確な表を使用することをお勧めします。詳細については、Hollander and Wolfe (1973)2を参照してください。
表記
| 用語 | 説明 |
|---|---|
| nj | グループjに含まれる観測値の数 |
| N | 総サンプルサイズ |
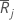 | グループjでの順位の平均 |
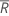 | すべての順位の平均 |
| ti | i番目の同順位のセットに含まれる同順位値の数 |
1 E.L. Lehmann (1975). Nonparametrics: Statistical Methods Based on Ranks, Holden-Day.
2 M. Hollander and D.A. Wolfe (1973). Nonparametric Statistical Methods, John Wiley & Sons, Inc.
