使用する方法を選択します。
直説法のp値
Minitabでは、二項分布を使用して、サイズ50（n ≤ 50）までのサンプルのp値を計算します。サンプルサイズがn（仮説の中央値と等しい観測値すべてを省略した後）で、帰無仮説における発生確率p = 0.5の場合、p値の計算方法は対立仮説によって異なります。
| 対立仮説 | p値 |
|---|---|
| H1: 中央値 > 仮説中央値 |  |
| H1: 中央値 < 仮説中央値 |  |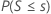
| H1: 中央値 ≠ 仮説中央値 |  |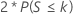
表記
| 用語 | 説明 |
|---|---|
| n | 仮説の中央値と等しい観測値すべてを省略した後のデータ点の観測数 |
| s | 仮説の中央値より大きいデータ点の観測数 |
| S | 試行回数がnで事象の確率が0.5の二項分布（B(n,0.5)）に従う確率変数 |
| k |  |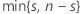
正規近似法のp値
Minitabでは、二項分布への正規近似を使用して、50（n ≤ 50）より大きいサンプルのp値を計算します。具体的には、次のようになります。
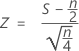は、平均値0および標準偏差1、N(0,1)として、ほぼ正規分布のように分布します。
ここで、中央値より上の観測値の数Sは、帰無仮説において試行回数がnで成功の確率p = 0.5の二項分布（B(n, 0.5)）です。
3つの対立仮説の正規近似p値で、連続量修正値0.5を使用します。
| 対立仮説 | p値 |
|---|---|
| H1: 中央値 > 仮説中央値 |  |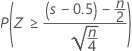
| H1: 中央値 < 仮説中央値 |  |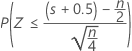
| H1: 中央値 ≠ 仮説中央値 |  |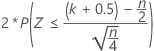
表記
| 用語 | 説明 |
|---|---|
| n | 仮説の中央値と等しい観測値すべてを省略した後のデータ点の観測数 |
| s | 仮説の中央値より大きいデータ点の観測数 |
| S | 試行回数がnで成功の確率がp = 0.5の二項分布（B(n,0.5)）に従う確率変数 |
| k |  |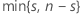
信頼区間
符号検定の統計量は離散するため、1サンプル符号検定では、指定した信頼水準が必ず達成されるとは限りません。このためMinitabでは、さまざまなレベルの精度で2つの信頼区間を計算します。
手順
- Minitabにより、X(1) < X(2) < ... < X(n)のように観測値が順序付けされます。ここで、X(i )はi番目に小さな観測値です。
- 指定した信頼水準（Y）の場合、最初の区間は信頼度がY以下の最も近い正確な区間です。3番目の区間は、信頼度がY以上の最も近い正確な区間です。次のように、dが最大の整数だとします。
- P (B < d) < (1 – γ) / 2
Bは、パラメータサンプルサイズがnで、発生確率p = 0.5の二項分布です。
- 最初の区間はX(d + 1)～X(n – d)、および3番目の区画はX(d )～X(n – d + 1)です。
- Minitabでは、Hettmansperger and Sheather1によって開発された非線形の内挿法（NLI）によって中間の信頼区間を計算します。γd + 1が最初の区間の信頼水準、γdが3番目の区間の信頼水準であるとします。
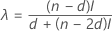
内挿法区間の最下端は、次の式で得られます。
- X(d) + λ (X(d + 1)– X(d))
最上端は、次の式で得られます。
- X(n – d + 1)– λ (X(n – d + 1)– X(n – d))
1 T.P. Hettmansperger and S.J. Sheather (1986). "Confidence Intervals Based on Interpolated Order Statistics," Statistics and Probability Letters, 4(2), 75-79.
