次の方法と計算式は、検定平均値と参照平均値の比を検定する場合に使用されます。
比
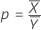
表記
| 用語 | 説明 |
|---|---|
| ρ | 比 |
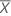 | 検定平均値 |
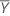 | 参照平均値 |
同等性限界
k1を下限について指定する値、k2を上限について指定する値とします。デフォルトでは、下側同等性限界δ1は次のように求められます。
上側同等性限界δ2は次のように求められます。
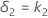
自由度（DF）
表記
| 用語 | 説明 |
|---|---|
| v | 自由度 |
| n | 観測値のペアの数 |
S12
S12は、X値とY値のサンプル共分散を表します。この値は、信頼区間およびt値の計算に使用されます。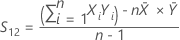 
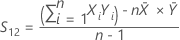
表記
| 用語 | 説明 |
|---|---|
| Xi | 検定サンプルに含まれるi番目の観測値。したがって、（Xi, Yi）はi番目の観測値のペア |
| Yi | 参照サンプルに含まれるi番目の観測値。したがって、（Xi, Yi）はi番目の観測値のペア |
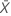 | 検定サンプルの平均 |
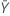 | 参照サンプルの平均 |
| n | 観測値のペアの数 |
信頼区間
次の2つの条件のいずれかを満たさない場合、Minitabは信頼区間（CI）を計算できません。
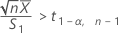
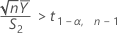
条件を満たす場合、Minitabは分析に使用する方法に基づいて信頼区間を計算します。
- 100(1 - α)%信頼区間
デフォルトでは、Minitabは次のようにρの100(1 - α)%信頼区間を計算します。
CI = [min(C, ρL), max(C, ρU)]
ここで、
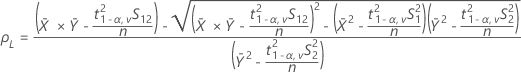
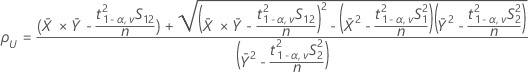
- 100(1 - 2α)%信頼区間
100(1 – 2α)%信頼区間を使用するオプションを選択した場合、信頼区間は次のように求められます。
CI = [ρL, ρU] - 片側区間
検定平均値/参照平均値 > 下側限界の仮説の場合、100(1 - α)%の下限はρLに等しくなります。
検定平均値/参照平均値 < 上側限界の仮説の場合、100(1 - α)%の上限はρUに等しくなります。
表記
| 用語 | 説明 |
|---|---|
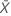 | 検定サンプルの平均 |
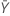 | 参照サンプルの平均 |
| S12 | X値とY値のサンプル共分散 |
| S1 | 検定サンプルの標準偏差 |
| n | サンプルサイズ |
| S2 | 参照サンプルの標準偏差 |
| δ1 | 下側同等性限界 |
| δ2 | 上側同等性限界 |
| v | 自由度 |
| α | 検定の有意水準（アルファ） |
| t1-α,v | 自由度vのt分布に対する上側の1 – α棄却限界値 |
t値
t1を仮説
のt値とし、t2を仮説
のt値とします。ここで、
は検定母集団の平均と参照母集団の平均の比です。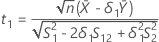 
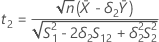
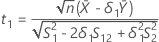
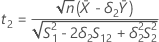
のt値とし、t2を仮説のt値とします。ここで、は検定母集団の平均と参照母集団の平均の比です。 表記
| 用語 | 説明 |
|---|---|
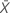 | 検定サンプルの平均 |
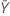 | 参照サンプルの平均 |
| S1 | 検定サンプルの標準偏差 |
| S2 | 参照サンプルの標準偏差 |
| S12 | X値とY値の相関 |
| n | 観測値のペアの数 |
| δ1 | 下側同等性限界 |
| δ2 | 上側同等性限界 |
| Λ | 検定母集団の平均と参照母集団の平均の未知の比 |
p値
それぞれの帰無仮説の確率PH0は、次のように求められます。
の場合、次のようになります。
| H0 | p値 |
|---|---|
 |
 |
 |
 |
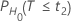表記
| 用語 | 説明 |
|---|---|
| Λ | 検定母集団の平均と参照母集団の平均の未知の比 |
| δ1 | 下側同等性限界 |
| δ2 | 上側同等性限界 |
| v | 自由度 |
| T | 自由度vのt分布 |
| t1 | 次の仮説のt値:  |
| t2 | 次の仮説のt値:  |
注
t値の計算方法については、t値に関するセクションを参照してください。
