差
平均間の差の仮説を選択した場合、サンプルから検定平均値と参照平均値の差が表示されます。
解釈
検定サンプルの平均は、検定母集団の平均の推定値です。参照サンプルの平均は、参照母集団の平均の推定値です。したがって、サンプル平均間の差によって、検定母集団の平均と参照母集団の平均の差の推定値が得られます。
差は母集団全体ではなくサンプルデータに基づいているため、検定母集団の平均と参照母集団の平均との差と等しいと確信することはできません。母集団の推定値の精度を評価するには、信頼区間を使用できます。
標準偏差
差の標準偏差(StDev)とは、散布度、つまり対応のある差が対応のある差の平均を基準にしてどれだけ異なるかを表します。
解釈
差の標準偏差を使用して、対応のある差が対応のある差の平均からどれだけ広がっているかを判断します。値が高い場合、変動性が高い、つまりデータの「雑音」が大きいことを示します。
差の標準偏差は、差の標準誤差を計算するために使用されます。
標準誤差
差の標準誤差(SE)は、同じ母集団からサンプルを繰り返し抜き取った場合に得られる参照平均値と検定平均値の差の変動性を推定します。差の標準誤差ではサンプル間の変動性が推定され、標準偏差では単一サンプル内の変動性が測定されます。
たとえば、サンプル検定平均値とサンプル参照平均値の差が−0.12122ユニットであるとします。10個のデータ値の検定サンプルの標準偏差は0.26138です。9個のデータ値の参照サンプルの標準偏差は0.58064です。差の標準誤差は、和(0.58064/10 + 0.26138/9)の平方根で、0.20324となります。同じ母集団から同じサイズのランダムサンプルを複数収集すると、サンプル間の差の標準偏差はおよそ0.20324になります。
解釈
差の標準誤差を使用して、サンプル平均間の差によって検定母集団の平均と参照母集団の平均の差が推定される精度を判断します。
標準誤差の値が低い場合、推定値の精度が高いことを示します。通常、標準偏差が大きいと、差の標準誤差が大きくなり、推定値の精度が低くなります。サンプルサイズが大きいと、差の標準誤差が小さくなり、推定値の精度が高くなります。
Minitabは、差の標準誤差を使用して検定統計量(t値)を計算します。
比
平均値の比の仮説を選択した場合、検定サンプルの平均値と参照サンプルの平均値との比が計算されます。
解釈
検定サンプルの平均は、検定母集団の平均の推定値です。参照サンプルの平均は、参照母集団の平均の推定値です。したがって、サンプル平均間の比によって、検定母集団の平均と参照母集団の平均の比の推定値が得られます。
比は母集団全体ではなくサンプルデータに基づいているため、母集団の比に等しいと確信することはできません。母集団の推定値の精度を評価するには、信頼区間を使用できます。
信頼区間(CI)
信頼区間によって、検定母集団の平均と参照母集団の平均との差(または比)の値が含まれる可能性が高い範囲が得られます。下側信頼限界は、差(または比)がそれより大きい可能性が高い値を定義します。上側信頼限界は、差(または比)がそれより小さい可能性が高い値を定義します。
注
デフォルト設定を使用して同等性検定を実行する場合、Minitabには同等性の信頼区間が表示されます。デフォルト設定を変更し、信頼区間を計算するための代わりの方法を使用する場合、Minitabには標準の信頼区間が表示されます。これらの間隔の差についての詳細は、「同等性検定での信頼区間」を参照してください。
解釈
信頼区間を同等性限界と比較します。信頼区間が同等性限界内に完全に含まれている場合、検定母集団の平均は参照母集団の平均と同等であると言うことができます。信頼区間の一部が同等性限界を外れている場合、同等であると言うことはできません。
差: 平均(割引) - 平均(元の値)
| 差 | 標準誤差 | 95% 同等の CI | 同等性区間 |
|---|---|---|---|
| -0.12122 | 0.20324 | (-0.483449, 0.241005) | (-0.5, 0.5) |
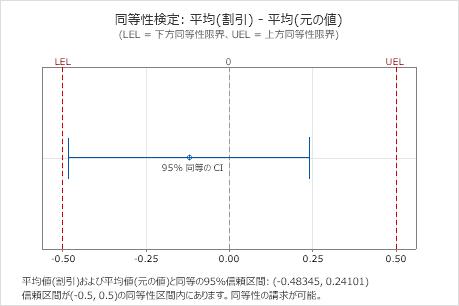
この結果で、95%信頼区間は下側同等性限界(LEL)と上側同等性限界(UEL)によって定義される同等区間に完全に含まれています。したがって、検定平均値は参照平均値と同等であると結論付けることができます。
下限
差(または比)の下側限界しか含まない対立仮説を選択した場合、Minitabは下側信頼境界値を表示します。下限は、検定母集団の平均と参照母集団の平均との差(または比)がそれより大きい可能性が高い値を示します。
解釈
下側信頼境界値を使用して、検定母集団の平均と参照母集団の平均との差(または比)は下側限界より大きいかどうかを判断します。 下側信頼境界値が下側限界よりも大きい場合、検定母集団の平均値と参照母集団の平均値との差(または比)が下側限界より大きいと主張することができます。
差: 平均(ジェネリック) - 平均(ブランド)
| 差 | 標準誤差 | 95%下限 | 下側限界 |
|---|---|---|---|
| -0.32104 | 0.060641 | -0.42735 | -0.42503 |
この結果で、差の95%の下側信頼境界値の下限は−0.42735で、下側限界の−0.42503より小さくなっています。したがって、検定母集団の平均と参照母集団の平均の差が下側限界より大きいと主張することはできません。
上限
差(または比)の上側限界しか含まない対立仮説を選択した場合、Minitabは上側信頼境界値を表示します。上限は、検定母集団の平均と参照母集団の平均との差(または比)がそれより小さい可能性が高い値を示します。
解釈
上側信頼境界値を使用して、検定母集団の平均と参照母集団の平均との差(または比)は上側限界より小さいかどうかを判断します。上側信頼境界値が上側限界未満の場合、検定母集団の平均値と参照母集団の平均値との差(または比)が上側限界より小さいと主張することができます。
差: 平均(ジェネリック) - 平均(ブランド)
| 差 | 標準誤差 | 95%上限 | 上側限界 |
|---|---|---|---|
| -0.32104 | 0.060641 | -0.21473 | 0.42503 |
この結果で、差の95%の上側信頼境界値は−0.21473で、上側限界の0.42503より小さくなっています。したがって、検定母集団の平均と参照母集団の平均の差が上側限界より小さいと95%信頼できます。
同等性区間
同等性区間は、同等と見なすのに十分なほど参照平均値に近い値の範囲です。区間は製品または工程に対する知識に基づき、下側同等性限界(LEL)と上側同等性限界(UEL)によって定義されます。
解釈
信頼区間を同等性限界と比較します。信頼区間が同等性限界内に完全に収まっている場合、検定母集団平均は参照母集団平均と同等であると主張できます。信頼区間の一部が同等性限界から外れている場合、同等だとの主張はできません。
差: 平均(ジェネリック) - 平均(ブランド)
| 差 | 標準誤差 | 95% 同等の CI | 同等性区間 |
|---|---|---|---|
| -0.32104 | 0.060641 | (-0.427349, 0) | (-0.425035, 0.425035) |

この結果で、95%信頼区間は下側同等性限界(LEL)と上側同等性限界(UEL)によって同等定義される区間に完全に収まっていません。信頼区間の下限は下側同等性限界を超えています。したがって、検定平均値が参照平均値と同等であると結論付けることはできません。
下側限界
検定平均値と参照平均値の差(または比)の許容可能性の下側限界。検定母集団の平均と参照母集団の平均の差(または比)は下側限界より大きい必要があります。
解釈
下側限界と下側信頼境界値を比較します。下側信頼境界値が下側限界よりも大きい場合、検定母集団の平均値と参照母集団の平均値との差(または比)が下側限界より大きいと主張することができます。
差: 平均(ジェネリック) - 平均(ブランド)
| 差 | 標準誤差 | 95%下限 | 下側限界 |
|---|---|---|---|
| -0.32104 | 0.060641 | -0.42735 | -0.42503 |
この結果で、差の95%の下側信頼境界値の下限は−0.42735で、下側限界の−0.42503より小さくなっています。したがって、検定母集団の平均と参照母集団の平均の差が下側限界より大きいと主張することはできません。
上側限界
検定平均値と参照平均値の差(または比)の許容可能性の上側限界。検定母集団の平均と参照母集団の平均の差(または比)は上側限界より小さい必要があります。
解釈
上側限界と上側信頼境界値を比較します。上側信頼境界値が上側限界未満の場合、検定母集団の平均値と参照母集団の平均値との差(または比)が上側限界より小さいと主張することができます。
差: 平均(ジェネリック) - 平均(ブランド)
| 差 | 標準誤差 | 95%上限 | 上側限界 |
|---|---|---|---|
| -0.32104 | 0.060641 | -0.21473 | 0.42503 |
この結果で、差の95%の上側信頼境界値は−0.21473で、上側限界の0.42503より小さくなっています。したがって、検定母集団の平均と参照母集団の平均の差が上側限界より小さいと95%信頼できます。
