次の方法と計算式は、検定平均値と参照平均値の比を検定する場合に使用されます。
比
下で示しているように、比ρは検定平均値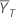 を参照平均値
を参照平均値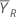 で割ったものに等しくなります。
で割ったものに等しくなります。
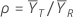


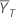 を参照平均値
を参照平均値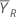 で割ったものに等しくなります。
で割ったものに等しくなります。
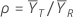


併合分散
参照期間の併合分散S2RRは、次のように求められます。
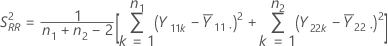
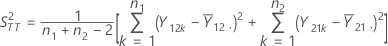
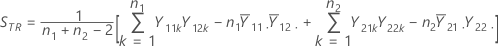
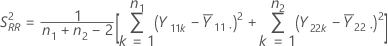
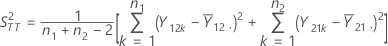
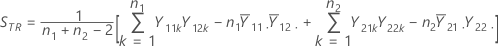
表記
| 用語 | 説明 |
|---|---|
| Yijk | 系列iでの期間jにおける参加者kの応答(詳細は、2x2交差計画の同等性検定で使用される一般的な概念の方法と計算式を参照してください) |
| ni | 系列iの参加者数 |
同等性の信頼区間
100(1-α)%信頼区間
次の2つの条件のいずれかを満たさない場合、Minitabは信頼区間(CI)を計算できません。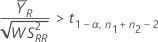

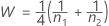
CI = [min(C, ρL), max(C, ρU)]
ここで、
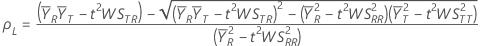
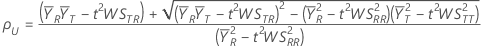
100(1-2α)%信頼区間
100(1 – 2α)%信頼区間を使用するオプションを選択した場合、信頼区間は次のように求められます。CI = [ρL, ρU]
片側区間
検定平均値/参照平均値 > 下側限界の仮説の場合、100(1 – α)%の下限はρLに等しくなります。
検定平均値/参照平均値 < 上側限界の仮説の場合、100(1 – α)%の上限はρUに等しくなります。
表記
| 用語 | 説明 |
|---|---|
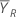 | 参照期間の平均(詳細については、比のセクションを参照) |
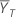 | 検定期間の平均(詳細については、比のセクションを参照) |
| ni | 系列iの参加者数 |
| v | 自由度 |
| α | 検定の有意水準(アルファ) |
| t1-α,v | 自由度vのt分布に対する上側の1 – α棄却限界値 |
t値
t1を仮説 のt値とし、t2を仮説
のt値とし、t2を仮説 のt値とします。ここで、
のt値とします。ここで、 は母集団の検定平均値と参照平均値の比です。t値は次のように計算されます。
は母集団の検定平均値と参照平均値の比です。t値は次のように計算されます。
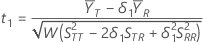
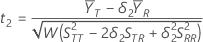
 のt値とし、t2を仮説
のt値とし、t2を仮説 のt値とします。ここで、
のt値とします。ここで、 は母集団の検定平均値と参照平均値の比です。t値は次のように計算されます。
は母集団の検定平均値と参照平均値の比です。t値は次のように計算されます。
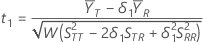
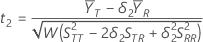
表記
| 用語 | 説明 |
|---|---|
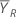 | 参照期間の平均(詳細については、比のセクションを参照) |
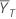 | 検定期間の平均(詳細については、比のセクションを参照) |
| δ1 | 下側同等性限界 |
| δ2 | 上側同等性限界 |
p値
それぞれの帰無仮説の確率PH0は、次のように求められます。
 の場合、次のようになります。
の場合、次のようになります。
| H0 | p値 |
|---|---|
 |
 |
 |
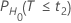 |
表記
| 用語 | 説明 |
|---|---|
| Λ | 検定母集団の平均と参照母集団の平均の未知の比 |
| δ1 | 下側同等性限界 |
| δ2 | 上側同等性限界 |
| v | 自由度 |
| T | 自由度vのt分布 |
| t1 | 次の仮説のt値:  |
| t2 | 次の仮説のt値:  |
注
t値の計算方法については、t値に関するセクションを参照してください。
