あるペットフード会社の食品科学エンジニアが、自社の人気キャットフードの新しい廉価な製造方法を試験します。エンジニアは、廉価な製造方法と通常のキャットフードのタンパク質含有量が同じであることを確認したいと考えています。そこで、両方の製造方法によるキャットフードのサンプル100グラム中のタンパク質含有量を測定し、±0.5グラム以内で等しいかどうかを試験します。
エンジニアは、2つの製造方法のタンパク質の平均の差が±0.5グラム以内かどうかを調べるために、2サンプル同等性検定を行います。2つの製造方法でタンパク質含有量の分散が等しいかどうかは分かっていません。
- サンプルデータキャットフードのタンパク質.MWXを開きます。
- を選択します。
- ドロップダウンリストから異なる列のサンプルを選択します。
- 検定サンプルに割引を入力します。
- 参照サンプルに元の値を入力します。
- 仮説から検定平均値 - 参照平均値を選択します。
- 何を判定しますか? (対立仮説)から下側限界 < 検定平均値 - 参照平均値 < 上側限界を選択します。
- 下側限界に–0.5を入力します。
- 上側限界に0.5を入力します。
- OKをクリックします。
結果を解釈する
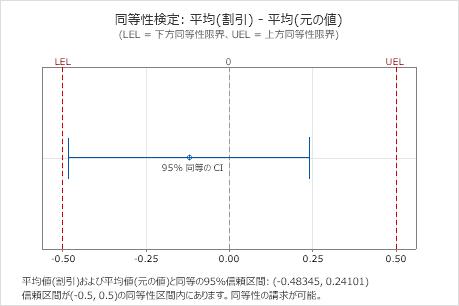
信頼区間は同等性区間に完全に含まれているため、エンジニアは2つの製造方法のキャットフードに同等量のタンパク質が含まれていると結論付けます。
方法
検定平均 = 割引の平均
参照平均 = 元の値の平均
等分散性は分析で仮定されていません。
参照平均 = 元の値の平均
等分散性は分析で仮定されていません。
記述統計量
| 変数 | N | 平均 | 標準偏差 | 平均の標準誤差 |
|---|---|---|---|---|
| 割引 | 10 | 33.971 | 0.58064 | 0.18361 |
| 元の値 | 9 | 34.092 | 0.26138 | 0.087127 |
差: 平均(割引) - 平均(元の値)
| 差 | 標準誤差 | 95% 同等の CI | 同等性区間 |
|---|---|---|---|
| -0.12122 | 0.20324 | (-0.483449, 0.241005) | (-0.5, 0.5) |
検定
| 帰無仮説: | 差 ≤ -0.5 または 差 ≥ 0.5 |
|---|---|
| 対立仮説: | -0.5 < 差 < 0.5 |
| α水準: | 0.05 |
| 帰無仮説 | 自由度 | t値 | p値 |
|---|---|---|---|
| 差 ≤ -0.5 | 12 | 1.8637 | 0.044 |
| 差 ≥ 0.5 | 12 | -3.0566 | 0.005 |